core_shell_cylinder

Right circular cylinder with a core-shell scattering length density profile.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld_core	Cylinder core scattering length density	10-6Å-2	4
sld_shell	Cylinder shell scattering length density	10-6Å-2	4
sld_solvent	Solvent scattering length density	10-6Å-2	1
radius	Cylinder core radius	Å	20
thickness	Cylinder shell thickness	Å	20
length	Cylinder length	Å	400
theta	cylinder axis to beam angle	degree	60
phi	rotation about beam	degree	60

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

The output of the 2D scattering intensity function for oriented core-shell cylinders is given by Kline [2]. The form factor is normalized by the particle volume. Note that in this model the shell envelops the entire core so that besides a “sleeve” around the core, the shell also provides two flat end caps of thickness = shell thickness. In other words the length of the total cylinder is the length of the core cylinder plus twice the thickness of the shell. If no end caps are desired one should use the core_shell_bicelle and set the thickness of the end caps (in this case the “thick_face”) to zero.

\[I(q,\alpha) = \frac{\text{scale}}{V_s} F^2(q,\alpha).sin(\alpha) + \text{background}\]

where

\[\begin{split}F(q,\alpha) = &\ (\rho_c - \rho_s) V_c \frac{\sin \left( q \tfrac12 L\cos\alpha \right)} {q \tfrac12 L\cos\alpha} \frac{2 J_1 \left( qR\sin\alpha \right)} {qR\sin\alpha} \\ &\ + (\rho_s - \rho_\text{solv}) V_s \frac{\sin \left( q \left(\tfrac12 L+T\right) \cos\alpha \right)} {q \left(\tfrac12 L +T \right) \cos\alpha} \frac{ 2 J_1 \left( q(R+T)\sin\alpha \right)} {q(R+T)\sin\alpha}\end{split}\]

and

\[V_s = \pi (R + T)^2 (L + 2T)\]

and \(\alpha\) is the angle between the axis of the cylinder and \(\vec q\), \(V_s\) is the total volume (i.e. including both the core and the outer shell), \(V_c\) is the volume of the core, \(L\) is the length of the core, \(R\) is the radius of the core, \(T\) is the thickness of the shell, \(\rho_c\) is the scattering length density of the core, \(\rho_s\) is the scattering length density of the shell, \(\rho_\text{solv}\) is the scattering length density of the solvent, and background is the background level. The outer radius of the shell is given by \(R+T\) and the total length of the outer shell is given by \(L+2T\). \(J_1\) is the first order Bessel function.

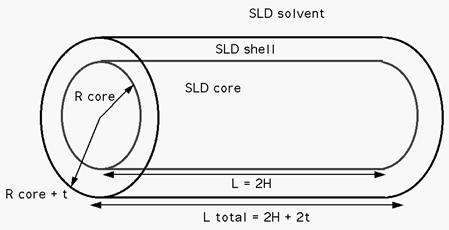
Fig. 19 Core shell cylinder schematic.

To provide easy access to the orientation of the core-shell cylinder, we define the axis of the cylinder using two angles \(\theta\) and \(\phi\). (see cylinder model)

NB: The 2nd virial coefficient of the cylinder is calculated based on the radius and 2 length values, and used as the effective radius for \(S(q)\) when \(P(q) \cdot S(q)\) is applied.

The \(\theta\) and \(\phi\) parameters are not used for the 1D output.

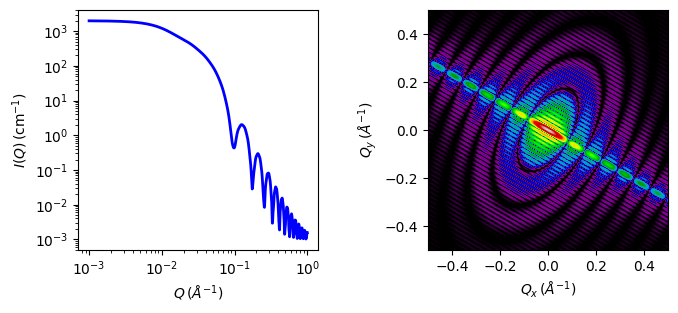
Fig. 20 1D and 2D plots corresponding to the default parameters of the model.

Source

core_shell_cylinder.py \(\ \star\ \) core_shell_cylinder.c \(\ \star\ \) gauss76.c \(\ \star\ \) sas_J1.c \(\ \star\ \) polevl.c

Reference

See also Livsey [1] and Onsager [3].

[1]

I Livsey, J. Chem. Soc., Faraday Trans. 2, 83 (1987) 1445-1452

[2]

S R Kline, J Appl. Cryst., 39 (2006) 895

[3]

12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Paul Kienzle Date: Aug 8, 2016

• Last Reviewed by: Richard Heenan Date: March 18, 2016