ellipsoid

Ellipsoid of revolution with uniform scattering length density.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld	Ellipsoid scattering length density	10-6Å-2	4
sld_solvent	Solvent scattering length density	10-6Å-2	1
radius_polar	Polar radius	Å	20
radius_equatorial	Equatorial radius	Å	400
theta	ellipsoid axis to beam angle	degree	60
phi	rotation about beam	degree	60

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

The form factor is normalized by the particle volume

Definition

The output of the 2D scattering intensity function for oriented ellipsoids is given by (Feigin, 1987)

\[P(q,\alpha) = \frac{\text{scale}}{V} F^2(q,\alpha) + \text{background}\]

where

\[F(q,\alpha) = \Delta \rho V \frac{3(\sin qr - qr \cos qr)}{(qr)^3}\]

for

\[r = \left[ R_e^2 \sin^2 \alpha + R_p^2 \cos^2 \alpha \right]^{1/2}\]

\(\alpha\) is the angle between the axis of the ellipsoid and \(\vec q\), \(V = (4/3)\pi R_pR_e^2\) is the volume of the ellipsoid, \(R_p\) is the polar radius along the rotational axis of the ellipsoid, \(R_e\) is the equatorial radius perpendicular to the rotational axis of the ellipsoid and \(\Delta \rho\) (contrast) is the scattering length density difference between the scatterer and the solvent.

For randomly oriented particles use the orientational average,

\[\langle F^2(q) \rangle = \int_{0}^{\pi/2}{F^2(q,\alpha)\sin(\alpha)\,d\alpha}\]

computed via substitution of \(u=\sin(\alpha)\), \(du=\cos(\alpha)\,d\alpha\) as

\[\langle F^2(q) \rangle = \int_0^1{F^2(q, u)\,du}\]

with

\[r = R_e \left[ 1 + u^2\left(R_p^2/R_e^2 - 1\right)\right]^{1/2}\]

For 2d data from oriented ellipsoids the direction of the rotation axis of the ellipsoid is defined using two angles \(\theta\) and \(\phi\) as for the cylinder orientation figure. For the ellipsoid, \(\theta\) is the angle between the rotational axis and the \(z\) -axis in the \(xz\) plane followed by a rotation by \(\phi\) in the \(xy\) plane, for further details of the calculation and angular dispersions see Oriented Particles.

NB: The 2nd virial coefficient of the solid ellipsoid is calculated based on the \(R_p\) and \(R_e\) values, and used as the effective radius for \(S(q)\) when \(P(q) \cdot S(q)\) is applied.

The \(\theta\) and \(\phi\) parameters are not used for the 1D output.

Validation

Validation of the code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006).

The implementation of the intensity for fully oriented ellipsoids was validated by averaging the 2D output using a uniform distribution \(p(\theta,\phi) = 1.0\) and comparing with the output of the 1D calculation.

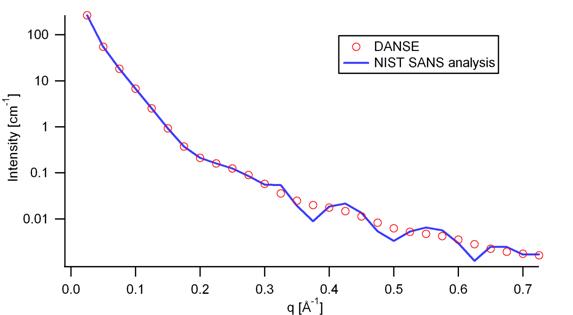
Fig. 40 Comparison of the intensity for uniformly distributed ellipsoids calculated from our 2D model and the intensity from the NIST SANS analysis software. The parameters used were: scale = 1.0, radius_polar = 20 Å, radius_equatorial = 400 Å, contrast = 3e-6 Å^-2, and background = 0.0 cm^-1.

The discrepancy above \(q\) = 0.3 cm^-1 is due to the way the form factors are calculated in the c-library provided by NIST. A numerical integration has to be performed to obtain \(P(q)\) for randomly oriented particles. The NIST software performs that integration with a 76-point Gaussian quadrature rule, which will become imprecise at high \(q\) where the amplitude varies quickly as a function of \(q\). The SasView result shown has been obtained by summing over 501 equidistant points. Our result was found to be stable over the range of \(q\) shown for a number of points higher than 500.

Model was also tested against the triaxial ellipsoid model with equal major and minor equatorial radii. It is also consistent with the cylinder model with polar radius equal to length and equatorial radius equal to radius.

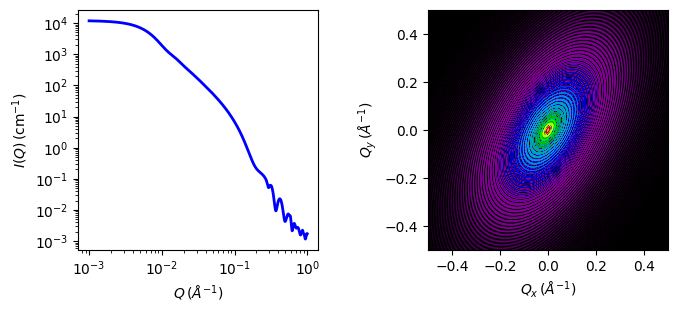
Fig. 41 1D and 2D plots corresponding to the default parameters of the model.

Source

ellipsoid.py \(\ \star\ \) ellipsoid.c \(\ \star\ \) gauss76.c \(\ \star\ \) sas_3j1x_x.c

References

1. L. A. Feigin and D. I. Svergun. Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum Press, New York, 1987

2. 1. Isihara. J. Chem. Phys., 18 (1950) 1446-1449

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Converted to sasmodels by: Helen Park Date: July 9, 2014

• Last Modified by: Paul Kienzle Date: March 22, 2017