flexible_cylinder_elliptical

Flexible cylinder wth an elliptical cross section and a uniform scattering length density.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
length	Length of the flexible cylinder	Å	1000
kuhn_length	Kuhn length of the flexible cylinder	Å	100
radius	Radius of the flexible cylinder	Å	20
axis_ratio	Axis_ratio (major_radius/minor_radius	None	1.5
sld	Cylinder scattering length density	10-6Å-2	1
sld_solvent	Solvent scattering length density	10-6Å-2	6.3

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model calculates the form factor for a flexible cylinder with an elliptical cross section and a uniform scattering length density. The non-negligible diameter of the cylinder is included by accounting for excluded volume interactions within the walk of a single cylinder. Inter-cylinder interactions are NOT provided for.

The form factor is normalized by the particle volume such that

\[P(q) = \text{scale} \left<F^2\right>/V + \text{background}\]

where the averaging \(\left<\ldots\right>\) is over all possible orientations of the flexible cylinder.

The 2D scattering intensity is the same as 1D, regardless of the orientation of the q vector which is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

Definitions

The function is calculated in a similar way to that for the flexible_cylinder model in reference [1] below using the author’s “Method 3 With Excluded Volume”.

The model is a parameterization of simulations of a discrete representation of the worm-like chain model of Kratky and Porod applied in the pseudo-continuous limit. See equations (13, 26-27) in the original reference for the details.

Note

There are several typos in the original reference that have been corrected by Chen et al (WRC) [2]. Details of the corrections are in the reference below. Most notably

• Equation (13): the term \((1 - w(QR))\) should swap position with \(w(QR)\)

• Equations (23) and (24) are incorrect; WRC has entered these into Mathematica and solved analytically. The results were then converted to code.

• Equation (27) should be \(q0 = max(a3/(Rg^2)^{1/2},3)\) instead of \(max(a3*b(Rg^2)^{1/2},3)\)

• The scattering function is negative for a range of parameter values and q-values that are experimentally accessible. A correction function has been added to give the proper behavior.

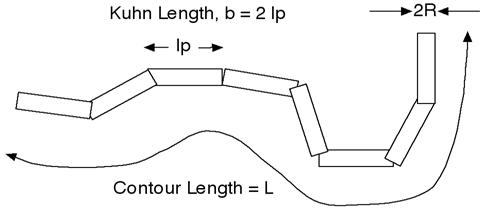
The chain of contour length, \(L\), (the total length) can be described as a chain of some number of locally stiff segments of length \(l_p\), the persistence length (the length along the cylinder over which the flexible cylinder can be considered a rigid rod). The Kuhn length \((b = 2*l_p)\) is also used to describe the stiffness of a chain.

The cross section of the cylinder is elliptical, with minor radius \(a\) . The major radius is larger, so of course, the axis_ratio must be greater than one. Simple constraints should be applied during curve fitting to maintain this inequality.

In the parameters, the \(sld\) and \(sld\_solvent\) represent the SLD of the chain/cylinder and solvent respectively. The scale, and the contrast are both multiplicative factors in the model and are perfectly correlated. One or both of these parameters must be held fixed during model fitting.

This is a model with complex behaviour depending on the ratio of \(L/b\) and the reader is strongly encouraged to read reference [1] before use.

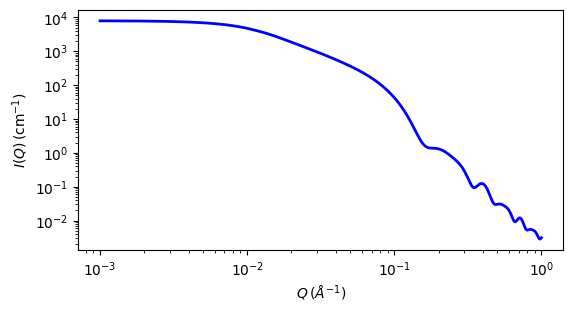
Fig. 30 1D plot corresponding to the default parameters of the model.

Source

flexible_cylinder_elliptical.py \(\ \star\ \) flexible_cylinder_elliptical.c \(\ \star\ \) wrc_cyl.c \(\ \star\ \) gauss76.c \(\ \star\ \) sas_J1.c \(\ \star\ \) polevl.c

References

1. J S Pedersen and P Schurtenberger. Scattering functions of semiflexible polymers with and without excluded volume effects. Macromolecules, 29 (1996) 7602-7612

2. W R Chen, P D Butler and L J Magid, Incorporating Intermicellar Interactions in the Fitting of SANS Data from Cationic Wormlike Micelles. Langmuir, 22(15) 2006 6539-6548

Authorship and Verification

• Author:

• Last Modified by: Richard Heenan Date: December, 2016

• Last Reviewed by: Steve King Date: March 26, 2019