lamellar_stack_paracrystal

Random lamellar sheet with paracrystal structure factor

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
thickness	sheet thickness	Å	33
Nlayers	Number of layers	None	20
d_spacing	lamellar spacing of paracrystal stack	Å	250
sigma_d	Sigma (polydispersity) of the lamellar spacing	Å	0
sld	layer scattering length density	10-6Å-2	1
sld_solvent	Solvent scattering length density	10-6Å-2	6.34

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model calculates the scattering from a stack of repeating lamellar structures. The stacks of lamellae (infinite in lateral dimension) are treated as a paracrystal to account for the repeating spacing. The repeat distance is further characterized by a Gaussian polydispersity. This model can be used for large multilamellar vesicles.

Definition

In the equations below,

• scale is used instead of the mass per area of the bilayer \(\Gamma_m\) (this corresponds to the volume fraction of the material in the bilayer, not the total excluded volume of the paracrystal),

• sld \(-\) sld_solvent is the contrast \(\Delta \rho\),

• thickness is the layer thickness \(t\),

• Nlayers is the number of layers \(N\),

• d_spacing is the average distance between adjacent layers \(\langle D \rangle\), and

• sigma_d is the relative standard deviation of the Gaussian layer distance distribution \(\sigma_D / \langle D \rangle\).

The scattering intensity \(I(q)\) is calculated as

\[I(q) = 2\pi\Delta\rho^2\Gamma_m\frac{P_\text{bil}(q)}{q^2} Z_N(q)\]

The form factor of the bilayer is approximated as the cross section of an infinite, planar bilayer of thickness \(t\) (compare the equations for the lamellar model).

\[P_\text{bil}(q) = \left(\frac{\sin(qt/2)}{qt/2}\right)^2\]

\(Z_N(q)\) describes the interference effects for aggregates consisting of more than one bilayer. The equations used are (3-5) from the Bergstrom reference:

\[Z_N(q) = \frac{1 - w^2}{1 + w^2 - 2w \cos(q \langle D \rangle)} + x_N S_N + (1 - x_N) S_{N+1}\]

where

\[S_N(q) = \frac{a_N}{N}[1 + w^2 - 2 w \cos(q \langle D \rangle)]^2\]

and

\[\begin{split}a_N &= 4w^2 - 2(w^3 + w) \cos(q \langle D \rangle) \\ &\quad - 4w^{N+2}\cos(Nq \langle D \rangle) + 2 w^{N+3}\cos[(N-1)q \langle D \rangle] + 2w^{N+1}\cos[(N+1)q \langle D \rangle]\end{split}\]

for the layer spacing distribution \(w = \exp(-\sigma_D^2 q^2/2)\).

Non-integer numbers of stacks are calculated as a linear combination of the lower and higher values

\[N_L = x_N N + (1 - x_N)(N+1)\]

The 2D scattering intensity is the same as 1D, regardless of the orientation of the \(q\) vector which is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

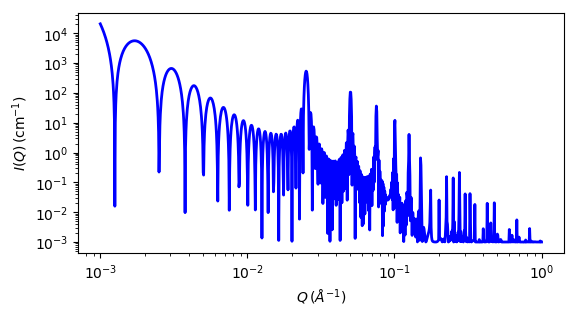
Fig. 50 1D plot corresponding to the default parameters of the model.

Source

lamellar_stack_paracrystal.py \(\ \star\ \) lamellar_stack_paracrystal.c

Reference

1. M Bergstrom, J S Pedersen, P Schurtenberger, S U Egelhaaf, J. Phys. Chem. B, 103 (1999) 9888-9897

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: