linear_pearls

Linear pearls model of scattering from spherical pearls.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
radius	Radius of the pearls	Å	80
edge_sep	Length of the string segment - surface to surface	Å	350
num_pearls	Number of the pearls	None	3
sld	SLD of the pearl spheres	10-6Å-2	1
sld_solvent	SLD of the solvent	10-6Å-2	6.3

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model provides the form factor for \(N\) spherical pearls of radius \(R\) linearly joined by short strings (or segment length or edge separation) \(l\) \((= A - 2R)\). \(A\) is the center-to-center pearl separation distance. The thickness of each string is assumed to be negligible.

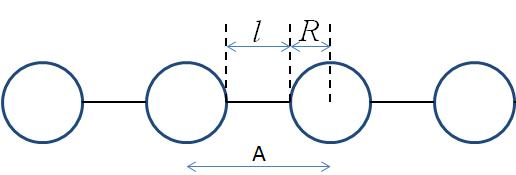
Definition

The output of the scattering intensity function for the linear_pearls model is given by (Dobrynin, 1996)

\[P(Q) = \frac{\text{scale}}{V}\left[ m_{p}^2 \left(N+2\sum_{n-1}^{N-1}(N-n)\frac{\sin(qnl)}{qnl}\right) \left( 3\frac{\sin(qR)-qR\cos(qR)}{(qr)^3}\right)^2\right]\]

where the mass \(m_p\) is \((SLD_{pearl}-SLD_{solvent})*(volume\ of\ N\ pearls)\). V is the total volume.

The 2D scattering intensity is the same as P(q) above, regardless of the orientation of the q vector.

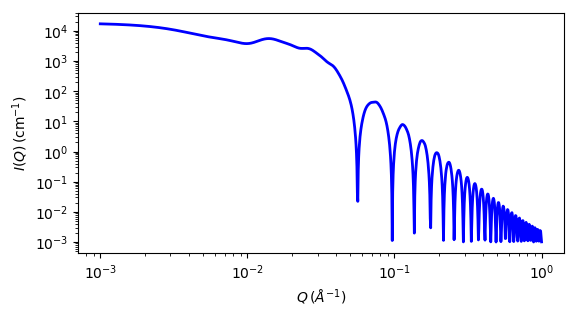
Fig. 82 1D plot corresponding to the default parameters of the model.

Source

linear_pearls.py \(\ \star\ \) linear_pearls.c \(\ \star\ \) sas_3j1x_x.c

References

1. A V Dobrynin, M Rubinstein and S P Obukhov, Macromol., 29 (1996) 2974-2979

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: