pearl_necklace

Colloidal spheres chained together with no preferential orientation

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
radius	Mean radius of the chained spheres	Å	80
edge_sep	Mean separation of chained particles	Å	350
thick_string	Thickness of the chain linkage	Å	2.5
num_pearls	Number of pearls in the necklace (must be integer)	none	3
sld	Scattering length density of the chained spheres	10-6Å-2	1
sld_string	Scattering length density of the chain linkage	10-6Å-2	1
sld_solvent	Scattering length density of the solvent	10-6Å-2	6.3

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model provides the form factor for a pearl necklace composed of two elements: N pearls (homogeneous spheres of radius R) freely jointed by M rods (like strings - with a total mass Mw = M * m_r + N * m_s, and the string segment length (or edge separation) l (= A - 2R)). A is the center-to-center pearl separation distance.

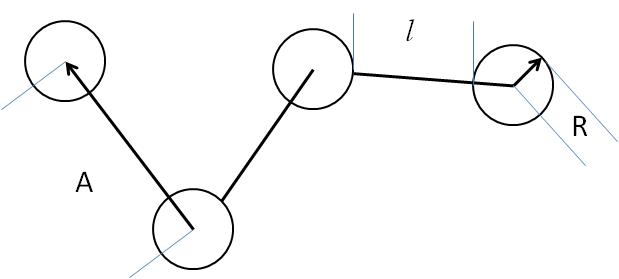
Fig. 32 Pearl Necklace schematic

Definition

The output of the scattering intensity function for the pearl_necklace is given by (Schweins, 2004)

\[I(q)=\frac{ \text{scale} }{V} \cdot \frac{(S_{ss}(q)+S_{ff}(q)+S_{fs}(q))} {(M \cdot m_f + N \cdot m_s)^2} + \text{bkg}\]

where

\[\begin{split}S_{ss}(q) &= 2m_s^2\psi^2(q)\left[\frac{N}{1-sin(qA)/qA}-\frac{N}{2}- \frac{1-(sin(qA)/qA)^N}{(1-sin(qA)/qA)^2}\cdot\frac{sin(qA)}{qA}\right] \\ S_{ff}(q) &= m_r^2\left[M\left\{2\Lambda(q)-\left(\frac{sin(ql/2)}{ql/2}\right)\right\}+ \frac{2M\beta^2(q)}{1-sin(qA)/qA}-2\beta^2(q)\cdot \frac{1-(sin(qA)/qA)^M}{(1-sin(qA)/qA)^2}\right] \\ S_{fs}(q) &= m_r \beta (q) \cdot m_s \psi (q) \cdot 4\left[ \frac{N-1}{1-sin(qA)/qA}-\frac{1-(sin(qA)/qA)^{N-1}}{(1-sin(qA)/qA)^2} \cdot \frac{sin(qA)}{qA}\right] \\ \psi(q) &= 3 \cdot \frac{sin(qR)-(qR)\cdot cos(qR)}{(qR)^3} \\ \Lambda(q) &= \frac{\int_0^{ql}\frac{sin(t)}{t}dt}{ql} \\ \beta(q) &= \frac{\int_{qR}^{q(A-R)}\frac{sin(t)}{t}dt}{ql}\end{split}\]

where the mass m_i is (SLD_i - SLD_solvent) * (volume of the N pearls/rods). V is the total volume of the necklace.

Note

num_pearls must be an integer.

The 2D scattering intensity is the same as \(P(q)\) above, regardless of the orientation of the q vector.

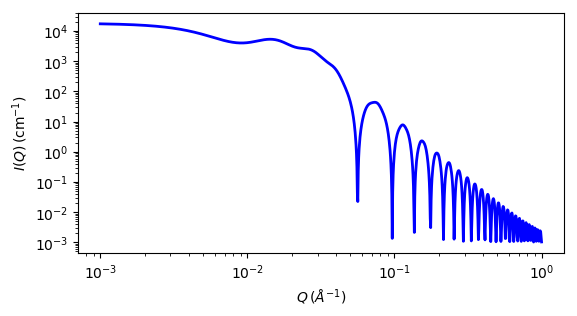
Fig. 33 1D plot corresponding to the default parameters of the model.

Source

pearl_necklace.py \(\ \star\ \) pearl_necklace.c \(\ \star\ \) sas_3j1x_x.c \(\ \star\ \) sas_Si.c

References

1. R Schweins and K Huber, Particle Scattering Factor of Pearl Necklace Chains, Macromol. Symp. 211 (2004) 25-42 2004

2. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author:

• Last Modified by: Andrew Jackson Date: March 28, 2019

• Last Reviewed by: Steve King Date: March 28, 2019