two_power_law

This model calculates an empirical functional form for SAS data characterized by two power laws.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
coefficent_1	coefficent A in low Q region	None	1
crossover	crossover location	Å-1	0.04
power_1	power law exponent at low Q	None	1
power_2	power law exponent at high Q	None	4

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

The scattering intensity \(I(q)\) is calculated as

\[\begin{split}I(q) = \begin{cases} A q^{-m1} + \text{background} & q <= q_c \\ C q^{-m2} + \text{background} & q > q_c \end{cases}\end{split}\]

where \(q_c\) = the location of the crossover from one slope to the other, \(A\) = the scaling coefficient that sets the overall intensity of the lower Q power law region, \(m1\) = power law exponent at low Q, and \(m2\) = power law exponent at high Q. The scaling of the second power law region (coefficient C) is then automatically scaled to match the first by following formula:

\[C = \frac{A q_c^{m2}}{q_c^{m1}}\]

Note

Be sure to enter the power law exponents as positive values!

For 2D data the scattering intensity is calculated in the same way as 1D, where the \(q\) vector is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

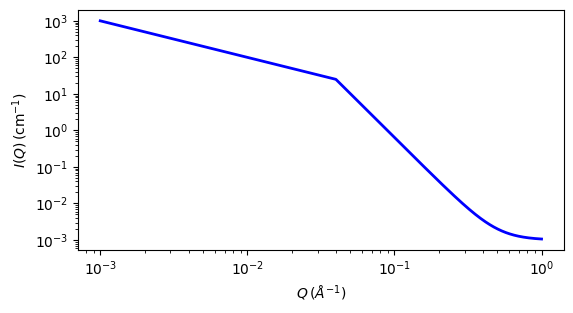
Fig. 125 1D plot corresponding to the default parameters of the model.

Source

two_power_law.py

References

None.

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Wojciech Wpotrzebowski Date: February 18, 2016

• Last Reviewed by: Paul Butler Date: March 21, 2016