vesicle

Vesicle model representing a hollow sphere

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld	vesicle shell scattering length density	10-6Å-2	0.5
sld_solvent	solvent scattering length density	10-6Å-2	6.36
volfraction	volume fraction of shell	None	0.05
radius	vesicle core radius	Å	100
thickness	vesicle shell thickness	Å	30

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

This model provides the form factor, P(q), for an unilamellar vesicle and is effectively identical to the hollow sphere reparameterized to be more intuitive for a vesicle and normalizing the form factor by the volume of the shell. The 1D scattering intensity is calculated in the following way [1]:

\[P(q) = \frac{\phi}{V_\text{shell}} \left[ \frac{3V_{\text{core}}({\rho_{\text{solvent}} - \rho_{\text{shell}})j_1(qR_{\text{core}})}}{qR_{\text{core}}} + \frac{3V_{\text{tot}}(\rho_{\text{shell}} - \rho_{\text{solvent}}) j_1(qR_{\text{tot}})}{qR_{\text{tot}}} \right]^2 + \text{background}\]

where \(\phi\) is the volume fraction of shell material, \(V_{shell}\) is the volume of the shell, \(V_{\text{cor}}\) is the volume of the core, \(V_{\text{tot}}\) is the total volume, \(R_{\text{core}}\) is the radius of the core, \(R_{\text{tot}}\) is the outer radius of the shell, \(\rho_{\text{solvent}}\) is the scattering length density of the solvent (which is the same as for the core in this case), \(\rho_{\text{scale}}\) is the scattering length density of the shell, background is a flat background level (due for example to incoherent scattering in the case of neutrons), and \(j_1\) is the spherical Bessel function \(j_1 = (\sin(x) - x \cos(x))/ x^2\).

The functional form is identical to a “typical” core-shell structure, except that the scattering is normalized by the volume that is contributing to the scattering, namely the volume of the shell alone, the scattering length density of the core is fixed the same as that of the solvent, the scale factor when the data are on an absolute scale is equivalent to the volume fraction of material in the shell rather than the entire core+shell sphere, and the parameterization is done in terms of the core radius = \(R_{\text{core}}\) and the shell thickness = \(R_{\text{tot}} - R_{\text{core}}\).

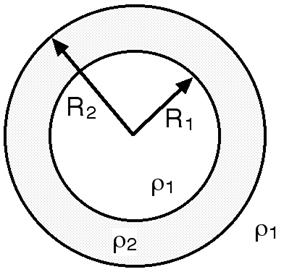
Fig. 98 Vesicle geometry.

The 2D scattering intensity is the same as P(q) above, regardless of the orientation of the q vector which is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

NB: The outer most radius (= radius + thickness) is used as the effective radius for S(Q) when P(Q) * S(Q) is applied.

Fig. 99 1D plot corresponding to the default parameters of the model.

Source

vesicle.py \(\ \star\ \) vesicle.c \(\ \star\ \) sas_3j1x_x.c

References

[1]

A Guinier and G. Fournet, Small-Angle Scattering of X-Rays, John Wiley and Sons, New York, (1955)

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Paul Butler Date: March 20, 2016

• Last Reviewed by: Paul Butler Date: September 7, 2018