fractal

Calculates the scattering from fractal-like aggregates of spheres following theTexiera reference.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
volfraction	volume fraction of blocks	None	0.05
radius	radius of particles	Å	5
fractal_dim	fractal dimension	None	2
cor_length	cluster correlation length	Å	100
sld_block	scattering length density of particles	10-6Å-2	2
sld_solvent	scattering length density of solvent	10-6Å-2	6.4

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition This model calculates the scattering from fractal-like aggregates of spherical building blocks according the following equation:

\[I(q) = \phi\ V_\text{block} (\rho_\text{block} - \rho_\text{solvent})^2 P(q)S(q) + \text{background}\]

where \(\phi\) is The volume fraction of the spherical “building block” particles of radius \(R_0\), \(V_{block}\) is the volume of a single building block, \(\rho_{solvent}\) is the scattering length density of the solvent, and \(\rho_{block}\) is the scattering length density of the building blocks, and P(q), S(q) are the scattering from randomly distributed spherical particles (the building blocks) and the interference from such building blocks organized in a fractal-like clusters. P(q) and S(q) are calculated as:

\[\begin{split}P(q)&= F(qR_0)^2 \\ F(q)&= \frac{3 (\sin x - x \cos x)}{x^3} \\ V_\text{particle} &= \frac{4}{3}\ \pi R_0 \\ S(q) &= 1 + \frac{D_f\ \Gamma\!(D_f-1)}{[1+1/(q \xi)^2\ ]^{(D_f -1)/2}} \frac{\sin[(D_f-1) \tan^{-1}(q \xi) ]}{(q R_0)^{D_f}}\end{split}\]

where \(\xi\) is the correlation length representing the cluster size and \(D_f\) is the fractal dimension, representing the self similarity of the structure. Note that S(q) here goes negative if \(D_f\) is too large, and the Gamma function diverges at \(D_f=0\) and \(D_f=1\).

Polydispersity on the radius is provided for.

For 2D data: The 2D scattering intensity is calculated in the same way as 1D, where the q vector is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

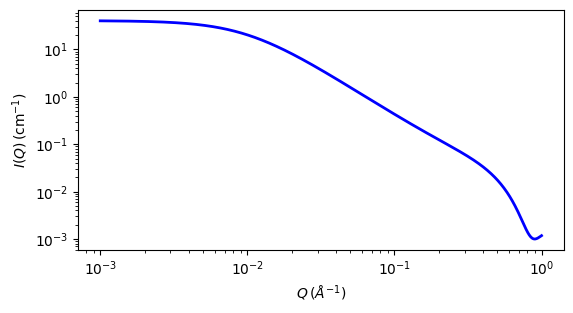
Fig. 104 1D plot corresponding to the default parameters of the model.

Source

fractal.py \(\ \star\ \) fractal.c \(\ \star\ \) fractal_sq.c \(\ \star\ \) sas_gamma.c \(\ \star\ \) sas_3j1x_x.c

References

1. J Teixeira, J. Appl. Cryst., 21 (1988) 781-785

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Converted to sasmodels by: Paul Butler Date: March 19, 2016

• Last Modified by: Paul Butler Date: March 12, 2017

• Last Reviewed by: Paul Butler Date: March 12, 2017