hardsphere¶
Hard sphere structure factor, with Percus-Yevick closure
Parameter |
Description |
Units |
Default value |
|---|---|---|---|
radius_effective |
effective radius of hard sphere |
Å |
50 |
volfraction |
volume fraction of hard spheres |
None |
0.2 |
The returned value is a dimensionless structure factor, \(S(q)\).
Calculates the interparticle structure factor for monodisperse spherical particles interacting through hard sphere (excluded volume) interactions. This \(S(q)\) may also be a reasonable approximation for other particle shapes that freely rotate (but see the note below), and for moderately polydisperse systems.
Note
This routine is intended for uncharged particles! For charged particles try using the hayter_msa \(S(q)\) instead.
Note
Earlier versions of SasView did not incorporate the so-called \(\beta(q)\) (“beta”) correction [1] for polydispersity and non-sphericity. This is only available in SasView versions 5.0 and higher.
radius_effective is the effective hard sphere radius. volfraction is the volume fraction occupied by the spheres.
In SasView the effective radius may be calculated from the parameters used in the form factor \(P(q)\) that this \(S(q)\) is combined with.
For numerical stability the computation uses a Taylor series expansion at very small \(qR\), but there may be a very minor glitch at the transition point in some circumstances.
This S(q) uses the Percus-Yevick closure relationship [2] where the interparticle potential \(U(r)\) is
where \(r\) is the distance from the center of a sphere of a radius \(R\).
For a 2D plot, the wave transfer is defined as
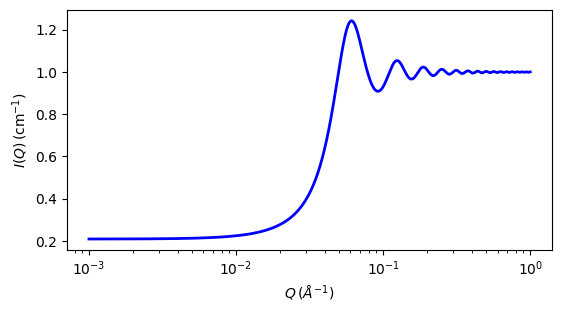
Fig. 129 1D plot corresponding to the default parameters of the model.¶
Source
hardsphere.py
\(\ \star\ \) hardsphere.c
References
M Kotlarchyk & S-H Chen, J. Chem. Phys., 79 (1983) 2461-2469
J K Percus, J Yevick, J. Phys. Rev., 110, (1958) 1
Authorship and Verification
Author:
Last Modified by:
Last Reviewed by: