lamellar_hg

Random lamellar phase with Head and Tail Groups

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
length_tail	Tail thickness ( total = H+T+T+H)	Å	15
length_head	Head thickness	Å	10
sld	Tail scattering length density	10-6Å-2	0.4
sld_head	Head scattering length density	10-6Å-2	3
sld_solvent	Solvent scattering length density	10-6Å-2	6

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model provides the scattering intensity, \(I(q)\), for a lyotropic lamellar phase where a random distribution in solution are assumed. The SLD of the head region is taken to be different from the SLD of the tail region.

Definition

The scattering intensity \(I(q)\) is

\[I(q) = 2\pi\frac{\text{scale}}{2(\delta_H + \delta_T)} P(q) \frac{1}{q^2}\]

The form factor \(P(q)\) is

\[P(q) = \frac{4}{q^2} \left\lbrace \Delta \rho_H \left[\sin[q(\delta_H + \delta_T)\ - \sin(q\delta_T)\right] + \Delta\rho_T\sin(q\delta_T) \right\rbrace^2\]

where \(\delta_T\) is length_tail, \(\delta_H\) is length_head, \(\Delta\rho_H\) is the head contrast (sld_head \(-\) sld_solvent), and \(\Delta\rho_T\) is tail contrast (sld \(-\) sld_solvent).

The total thickness of the lamellar sheet is \(a_H + \delta_T + \delta_T + \delta_H\). Note that in a non aqueous solvent the chemical “head” group may be the “Tail region” and vice-versa.

The 2D scattering intensity is calculated in the same way as 1D, where the \(q\) vector is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

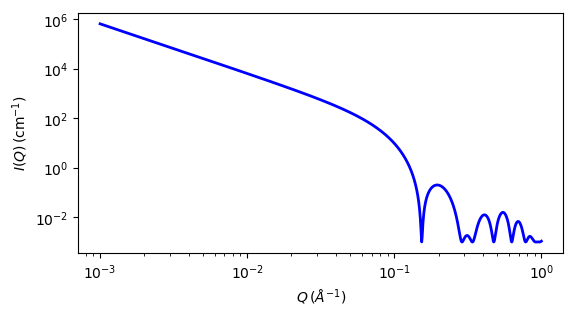
Fig. 47 1D plot corresponding to the default parameters of the model.

Source

lamellar_hg.py \(\ \star\ \) lamellar_hg.c

References

1. F Nallet, R Laversanne, and D Roux, J. Phys. II France, 3, (1993) 487-502

2. J Berghausen, J Zipfel, P Lindner, W Richtering, J. Phys. Chem. B, 105, (2001) 11081-11088

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: S King and P Butler Date April 17, 2014