cylinder

Right circular cylinder with uniform scattering length density.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld	Cylinder scattering length density	10-6Å-2	4
sld_solvent	Solvent scattering length density	10-6Å-2	1
radius	Cylinder radius	Å	20
length	Cylinder length	Å	400
theta	cylinder axis to beam angle	degree	60
phi	rotation about beam	degree	60

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

For information about polarised and magnetic scattering, see the Polarisation/Magnetic Scattering documentation.

Definition

The output of the 2D scattering intensity function for oriented cylinders is given by (Guinier, 1955)

\[I(q,\alpha) = \frac{\text{scale}}{V} F^2(q,\alpha) + \text{background}\]

where

\[F(q,\alpha) = 2 (\Delta \rho) V \frac{\sin \left(\tfrac12 qL\cos\alpha \right)} {\tfrac12 qL \cos \alpha} \frac{J_1 \left(q R \sin \alpha\right)}{q R \sin \alpha}\]

and \(\alpha\) is the angle between the axis of the cylinder and \(\vec q\), \(V =\pi R^2L\) is the volume of the cylinder, \(L\) is the length of the cylinder, \(R\) is the radius of the cylinder, and \(\Delta\rho\) (contrast) is the scattering length density difference between the scatterer and the solvent. \(J_1\) is the first order Bessel function.

For randomly oriented particles:

\[P(q)=F^2(q)=\int_{0}^{\pi/2}{F^2(q,\alpha)\sin(\alpha)d\alpha}\]

The output of the 1D scattering intensity function for randomly oriented cylinders is thus given by

\[I(q) = \frac{\text{scale}}{V} \int_0^{\pi/2} F^2(q,\alpha) \sin \alpha\ d\alpha + \text{background}\]

NB: The 2nd virial coefficient of the cylinder is calculated based on the radius and length values, and used as the effective radius for \(S(q)\) when \(P(q) \cdot S(q)\) is applied.

For 2d scattering from oriented cylinders, we define the direction of the axis of the cylinder using two angles \(\theta\) (note this is not the same as the scattering angle used in q) and \(\phi\). Those angles are defined in Fig. 21 , for further details see Oriented Particles.

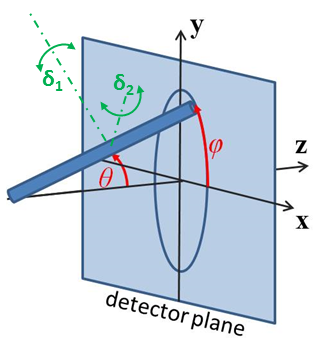
Fig. 21 Angles \(\theta\) and \(\phi\) orient the cylinder relative to the beam line coordinates, where the beam is along the \(z\) axis. Rotation \(\theta\), initially in the \(xz\) plane, is carried out first, then rotation \(\phi\) about the \(z\) axis. Orientation distributions are described as rotations about two perpendicular axes \(\delta_1\) and \(\delta_2\) in the frame of the cylinder itself, which when \(\theta = \phi = 0\) are parallel to the \(Y\) and \(X\) axes.

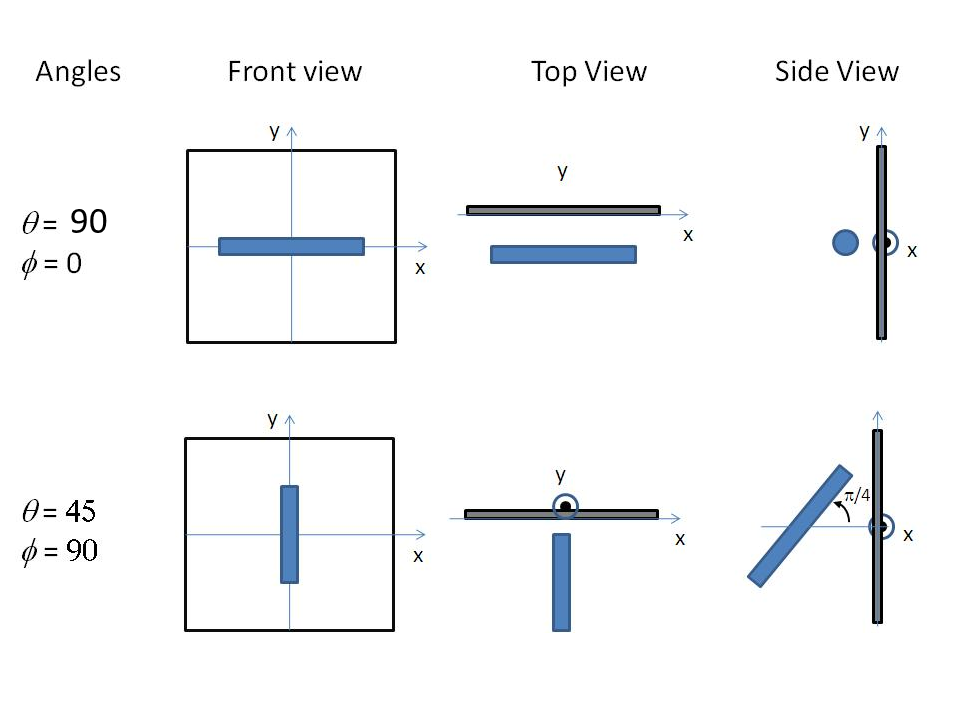
Fig. 22 Examples for oriented cylinders.

The \(\theta\) and \(\phi\) parameters to orient the cylinder only appear in the model when fitting 2d data.

Validation

Validation of the code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006). The implementation of the intensity for fully oriented cylinders was done by averaging over a uniform distribution of orientations using

\[P(q) = \int_0^{\pi/2} d\phi \int_0^\pi p(\theta) P_0(q,\theta) \sin \theta\ d\theta\]

where \(p(\theta,\phi) = 1\) is the probability distribution for the orientation and \(P_0(q,\theta)\) is the scattering intensity for the fully oriented system, and then comparing to the 1D result.

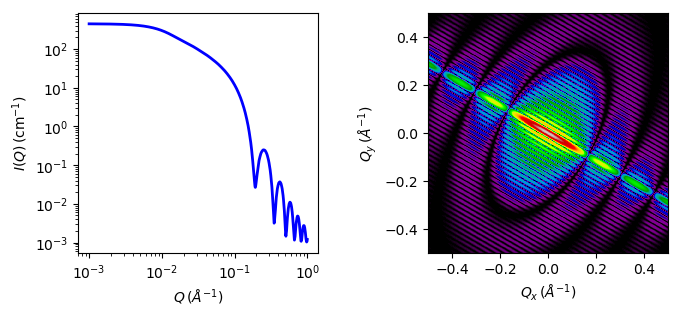
Fig. 23 1D and 2D plots corresponding to the default parameters of the model.

Source

cylinder.py \(\ \star\ \) cylinder.c \(\ \star\ \) gauss76.c \(\ \star\ \) sas_J1.c \(\ \star\ \) polevl.c

References

1. 10. Pedersen, Adv. Colloid Interface Sci., 70 (1997) 171-210

2. 7. Fournet, Bull. Soc. Fr. Mineral. Cristallogr., 74 (1951) 39-113

3. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author:

• Last Modified by: Paul Butler (docs only) November 10, 2022

• Last Reviewed by: