onion

Onion shell model with constant, linear or exponential density

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld_core	Core scattering length density	10-6Å-2	1
radius_core	Radius of the core	Å	200
sld_solvent	Solvent scattering length density	10-6Å-2	6.4
n_shells	number of shells (must be integer)	None	1
sld_in[n_shells]	scattering length density at the inner radius of shell k	10-6Å-2	1.7
sld_out[n_shells]	scattering length density at the outer radius of shell k	10-6Å-2	2
thickness[n_shells]	Thickness of shell k	Å	40
A[n_shells]	Decay rate of shell k	None	1

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model provides the form factor, \(P(q)\), for a multi-shell sphere where the scattering length density (SLD) of each shell is described by an exponential, linear, or constant function. The form factor is normalized by the volume of the sphere where the SLD is not identical to the SLD of the solvent. We currently provide up to 9 shells with this model.

Note

radius represents the core radius \(r_0\) and thickness[k] represents the thickness of the shell, \(r_{k+1} - r_k\).

Definition

The 1D scattering intensity is calculated in the following way

\[P(q) = [f]^2 / V_\text{particle}\]

where

\begin{align*} f &= f_\text{core} + \left(\sum_{\text{shell}=1}^N f_\text{shell}\right) + f_\text{solvent} \end{align*}

The shells are spherically symmetric with particle density \(\rho(r)\) and constant SLD within the core and solvent, so

\begin{align*} f_\text{core} &= 4\pi\int_0^{r_\text{core}} \rho_\text{core} \frac{\sin(qr)}{qr}\, r^2\,\mathrm{d}r &= 3\rho_\text{core} V(r_\text{core}) \frac{j_1(qr_\text{core})}{qr_\text{core}} \\ f_\text{shell} &= 4\pi\int_{r_{\text{shell}-1}}^{r_\text{shell}} \rho_\text{shell}(r)\frac{\sin(qr)}{qr}\,r^2\,\mathrm{d}r \\ f_\text{solvent} &= 4\pi\int_{r_N}^\infty \rho_\text{solvent}\frac{\sin(qr)}{qr}\,r^2\,\mathrm{d}r &= -3\rho_\text{solvent}V(r_N)\frac{j_1(q r_N)}{q r_N} \end{align*}

where the spherical Bessel function \(j_1\) is

\[j_1(x) = \frac{\sin(x)}{x^2} - \frac{\cos(x)}{x}\]

and the volume is \(V(r) = \frac{4\pi}{3}r^3\).

The volume of the particle is determined by the radius of the outer shell, so \(V_\text{particle} = V(r_N)\).

Now consider the SLD of a shell defined by

\[\begin{split}\rho_\text{shell}(r) = \begin{cases} B\exp\left(A(r-r_{\text{shell}-1})/\Delta t_\text{shell}\right) + C & \mbox{for } A \neq 0 \\ \rho_\text{in} = \text{constant} & \mbox{for } A = 0 \end{cases}\end{split}\]

An example of a possible SLD profile is shown below where \(\rho_\text{in}\) and \(\Delta t_\text{shell}\) stand for the SLD of the inner side of the \(k^\text{th}\) shell and the thickness of the \(k^\text{th}\) shell in the equation above, respectively.

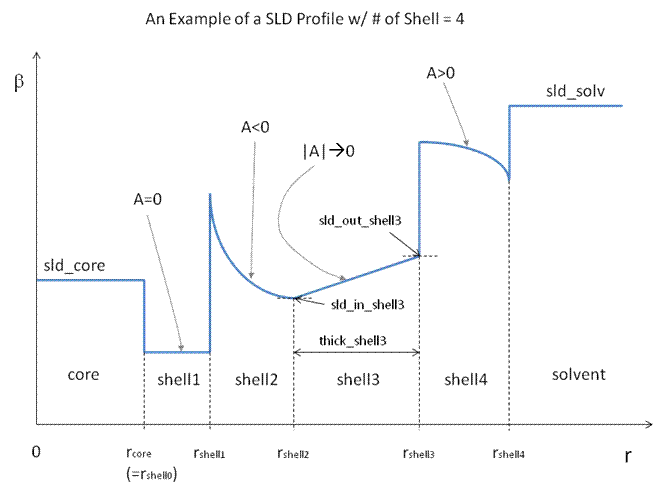
Fig. 87 Example of an onion model profile.

Exponential SLD profiles (\(A > 0\) or \(A < 0\)):

\[\begin{split}f_\text{shell} &= 4 \pi \int_{r_{\text{shell}-1}}^{r_\text{shell}} \left[ B\exp \left(A (r - r_{\text{shell}-1}) / \Delta t_\text{shell} \right) + C \right] \frac{\sin(qr)}{qr}\,r^2\,\mathrm{d}r \\ &= 3BV(r_\text{shell}) e^A h(\alpha_\text{out},\beta_\text{out}) - 3BV(r_{\text{shell}-1}) h(\alpha_\text{in},\beta_\text{in}) + 3CV(r_{\text{shell}}) \frac{j_1(\beta_\text{out})}{\beta_\text{out}} - 3CV(r_{\text{shell}-1}) \frac{j_1(\beta_\text{in})}{\beta_\text{in}}\end{split}\]

where

\begin{align*} B&=\frac{\rho_\text{out} - \rho_\text{in}}{e^A-1} & C &= \frac{\rho_\text{in}e^A - \rho_\text{out}}{e^A-1} \\ \alpha_\text{in} &= A\frac{r_{\text{shell}-1}}{\Delta t_\text{shell}} & \alpha_\text{out} &= A\frac{r_\text{shell}}{\Delta t_\text{shell}} \\ \beta_\text{in} &= qr_{\text{shell}-1} & \beta_\text{out} &= qr_\text{shell} \end{align*}

and

\[h(x,y) = \frac{x \sin(y) - y\cos(y)}{(x^2+y^2)y} - \frac{(x^2-y^2)\sin(y) - 2xy\cos(y)}{(x^2+y^2)^2y}\]

Linear SLD profile (\(A \sim 0\)):

For small \(A\), say, \(A = -0.0001\), the function converges to that of of a linear SLD profile with

\(\rho_\text{shell}(r) \approx A(r-r_{\text{shell}-1})/\Delta t_\text{shell})+B\),

which is equivalent to

\begin{align*} f_\text{shell} &= 3 V(r_\text{shell}) \frac{\Delta\rho_\text{shell}}{\Delta t_\text{shell}} \left[\frac{ 2 \cos(qr_\text{out}) + qr_\text{out} \sin(qr_\text{out}) }{ (qr_\text{out})^4 }\right] \\ &{} -3 V(r_\text{shell}) \frac{\Delta\rho_\text{shell}}{\Delta t_\text{shell}} \left[\frac{ 2\cos(qr_\text{in}) +qr_\text{in}\sin(qr_\text{in}) }{ (qr_\text{in})^4 }\right] \\ &{} +3\rho_\text{out}V(r_\text{shell}) \frac{j_1(qr_\text{out})}{qr_\text{out}} -3\rho_\text{in}V(r_{\text{shell}-1}) \frac{j_1(qr_\text{in})}{qr_\text{in}} \end{align*}

Constant SLD (\(A = 0\)):

When \(A = 0\) the exponential function has no dependence on the radius (meaning \(\rho_\text{out}\) is ignored in this case) and becomes flat. We set the constant to \(\rho_\text{in}\) for convenience, and thus the form factor contributed by the shells is

\[f_\text{shell} = 3\rho_\text{in}V(r_\text{shell}) \frac{j_1(qr_\text{out})}{qr_\text{out}} - 3\rho_\text{in}V(r_{\text{shell}-1}) \frac{j_1(qr_\text{in})}{qr_\text{in}}\]

The 2D scattering intensity is the same as \(P(q)\) above, regardless of the orientation of the \(q\) vector which is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

NB: The outer most radius is used as the effective radius for \(S(q)\) when \(P(q) S(q)\) is applied.

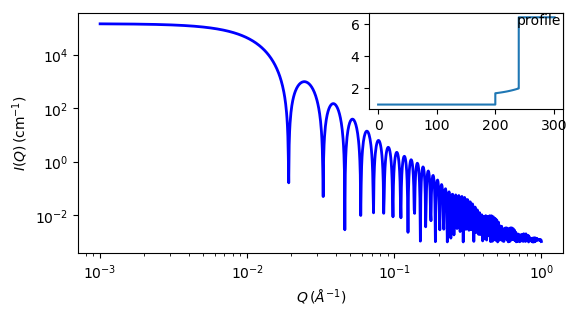
Fig. 88 1D plot corresponding to the default parameters of the model.

Source

onion.py \(\ \star\ \) onion.c \(\ \star\ \) sas_3j1x_x.c

References

1. L A Feigin and D I Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum Press, New York, 1987.

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: Steve King Date: March 28, 2019