barbell

Cylinder with spherical end caps

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld	Barbell scattering length density	10-6Å-2	4
sld_solvent	Solvent scattering length density	10-6Å-2	1
radius_bell	Spherical bell radius	Å	40
radius	Cylindrical bar radius	Å	20
length	Cylinder bar length	Å	400
theta	Barbell axis to beam angle	degree	60
phi	Rotation about beam	degree	60

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

Calculates the scattering from a barbell-shaped cylinder. Like capped_cylinder, this is a spherocylinder with spherical end caps that have a radius larger than that of the cylinder, but with the center of the end cap radius lying outside of the cylinder. See the diagram for the details of the geometry and restrictions on parameter values.

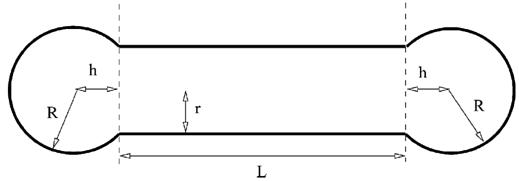
Fig. 1 Barbell geometry, where \(r\) is radius, \(R\) is radius_bell and \(L\) is length. Since the end cap radius \(R \geq r\) and by definition for this geometry \(h \ge 0\), \(h\) is then defined by \(r\) and \(R\) as \(h = \sqrt{R^2 - r^2}\)

The scattered intensity \(I(q)\) is calculated as

\[I(q) = \frac{\Delta \rho^2}{V} \left<A^2(q,\alpha).sin(\alpha)\right>\]

where the amplitude \(A(q,\alpha)\) with the rod axis at angle \(\alpha\) to \(q\) is given as

\[\begin{split}A(q) =&\ \pi r^2L \frac{\sin\left(\tfrac12 qL\cos\alpha\right)} {\tfrac12 qL\cos\alpha} \frac{2 J_1(qr\sin\alpha)}{qr\sin\alpha} \\ &\ + 4 \pi R^3 \int_{-h/R}^1 dt \cos\left[ q\cos\alpha \left(Rt + h + {\tfrac12} L\right)\right] \times (1-t^2) \frac{J_1\left[qR\sin\alpha \left(1-t^2\right)^{1/2}\right]} {qR\sin\alpha \left(1-t^2\right)^{1/2}}\end{split}\]

The \(\left<\ldots\right>\) brackets denote an average of the structure over all orientations. \(\left<A^2(q,\alpha)\right>\) is then the form factor, \(P(q)\). The scale factor is equivalent to the volume fraction of cylinders, each of volume, \(V\). Contrast \(\Delta\rho\) is the difference of scattering length densities of the cylinder and the surrounding solvent.

The volume of the barbell is

\[V = \pi r_c^2 L + 2\pi\left(\tfrac23R^3 + R^2h-\tfrac13h^3\right)\]

and its radius of gyration is

\[\begin{split}R_g^2 =&\ \left[ \tfrac{12}{5}R^4 + R^3\left(3L + \tfrac{18}{5} h\right) + R^2\left(L^2 + Lh + \tfrac25 h^2\right) + R\left(\tfrac14 L^3 + \tfrac12 L^2h - Lh^2\right) \right. \\ &\ \left. + Lh^4 - \tfrac12 L^2h^3 - \tfrac14 L^3h + \tfrac25 h^4\right] \left( 4R^2 + 3LR + 2Rh - 3Lh - 2h^2\right)^{-1}\end{split}\]

Note

The requirement that \(R \geq r\) is not enforced in the model! It is up to you to restrict this during analysis.

The 2D scattering intensity is calculated similar to the 2D cylinder model.

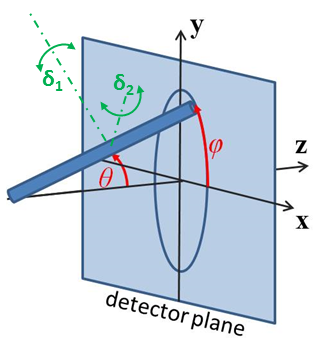
Fig. 2 Definition of the angles for oriented 2D barbells.

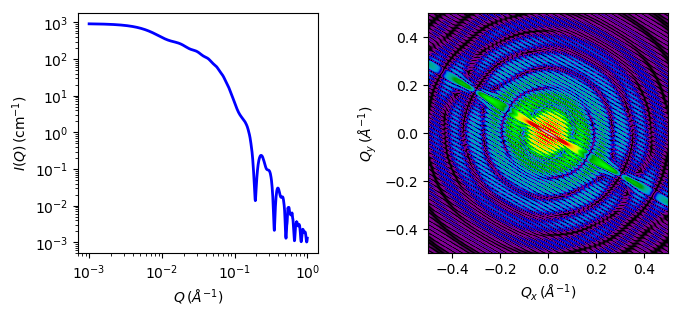
Fig. 3 1D and 2D plots corresponding to the default parameters of the model.

Source

barbell.py \(\ \star\ \) barbell.c \(\ \star\ \) gauss76.c \(\ \star\ \) sas_J1.c \(\ \star\ \) polevl.c

References

1. H Kaya, J. Appl. Cryst., 37 (2004) 223-230

2. H Kaya and N R deSouza, J. Appl. Cryst., 37 (2004) 508-509 (addenda and errata)

3. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Paul Butler Date: March 20, 2016

• Last Reviewed by: Richard Heenan Date: January 4, 2017