broad_peak

Broad peak on top of a power law decay

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
porod_scale	Power law scale factor	None	1e-05
porod_exp	Exponent of power law	None	3
peak_scale	Scale factor for broad peak	None	10
correlation_length	screening length	Å	50
peak_pos	Peak position in q	Å-1	0.1
width_exp	Exponent of peak width	None	2
shape_exp	Exponent of peak shape	None	1

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

This model calculates an empirical functional form for SAS data characterized by a broad scattering peak. Many SAS spectra are characterized by a broad peak even though they are from amorphous soft materials. For example, soft systems that show a SAS peak include copolymers, polyelectrolytes, multiphase systems, layered structures, etc.

The d-spacing corresponding to the broad peak is a characteristic distance between the scattering inhomogeneities (such as in lamellar, cylindrical, or spherical morphologies, or for bicontinuous structures).

The scattering intensity \(I(q)\) is calculated as

\[I(q) = \frac{A}{q^n} + \frac{C}{1 + (|q - q_0|\xi)^m}^p + B\]

Here the peak position is related to the d-spacing as \(q_0 = 2\pi / d_0\).

\(A\) is the Porod law scale factor, \(n\) the Porod exponent, \(C\) is the Lorentzian scale factor, \(m\) the exponent of \(q\), \(\xi\) the screening length, and \(B\) the flat background. \(p\) generalizes the model. With m = 2 and p = 1 the Lorentz model is obtained whereas for m = 2 and p = 2 the Broad-Peak model is identical to the Debye-Anderson-Brumberger (dab) model.

For 2D data the scattering intensity is calculated in the same way as 1D, where the \(q\) vector is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

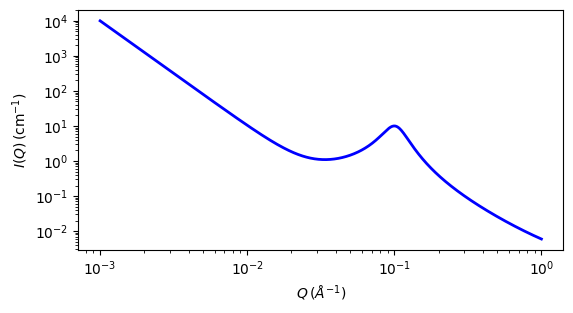
Fig. 101 1D plot corresponding to the default parameters of the model.

Source

broad_peak.py

References

None.

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Dirk Honecker Date: May 28, 2021

• Last Reviewed by: Richard Heenan Date: March 21, 2016