correlation_length

Calculates an empirical functional form for SAS data characterized by a low-Q signal and a high-Q signal.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
lorentz_scale	Lorentzian Scaling Factor	None	10
porod_scale	Porod Scaling Factor	None	1e-06
cor_length	Correlation length, xi, in Lorentzian	Å	50
porod_exp	Porod Exponent, n, in q^-n	None	3
lorentz_exp	Lorentzian Exponent, m, in 1/( 1 + (q.xi)^m)	None	2

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

The scattering intensity I(q) is calculated as

\[I(Q) = \frac{A}{Q^n} + \frac{C}{1 + (Q\xi)^m} + \text{background}\]

The first term describes Porod scattering from clusters (exponent = \(n\)) and the second term is a Lorentzian function describing scattering from polymer chains (exponent = \(m\)). This second term characterizes the polymer/solvent interactions and therefore the thermodynamics. The two multiplicative factors \(A\) and \(C\), and the two exponents \(n\) and \(m\) are used as fitting parameters. (Respectively porod_scale, lorentz_scale, porod_exp and lorentz_exp in the parameter list.) The remaining parameter \(\xi\) (cor_length in the parameter list) is a correlation length for the polymer chains. Note that when \(m=2\) this functional form becomes the familiar Lorentzian function. Some interpretation of the values of \(A\) and \(C\) may be possible depending on the values of \(m\) and \(n\).

For 2D data: The 2D scattering intensity is calculated in the same way as 1D, where the q vector is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

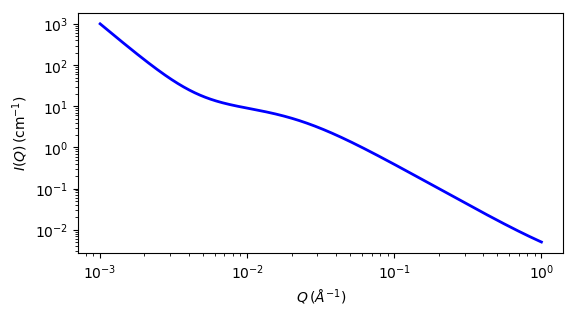
Fig. 102 1D plot corresponding to the default parameters of the model.

Source

correlation_length.py

References

1. B Hammouda, D L Ho and S R Kline, Insight into Clustering in Poly(ethylene oxide) Solutions, Macromolecules, 37 (2004) 6932-6937

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Steve King Date: September 24, 2019

• Last Reviewed by: