core_shell_parallelepiped

Rectangular solid with a core-shell structure.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld_core	Parallelepiped core scattering length density	10-6Å-2	1
sld_a	Parallelepiped A rim scattering length density	10-6Å-2	2
sld_b	Parallelepiped B rim scattering length density	10-6Å-2	4
sld_c	Parallelepiped C rim scattering length density	10-6Å-2	2
sld_solvent	Solvent scattering length density	10-6Å-2	6
length_a	Shorter side of the parallelepiped	Å	35
length_b	Second side of the parallelepiped	Å	75
length_c	Larger side of the parallelepiped	Å	400
thick_rim_a	Thickness of A rim	Å	10
thick_rim_b	Thickness of B rim	Å	10
thick_rim_c	Thickness of C rim	Å	10
theta	c axis to beam angle	degree	0
phi	rotation about beam	degree	0
psi	rotation about c axis	degree	0

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

Calculates the form factor for a rectangular solid with a core-shell structure. The thickness and the scattering length density of the shell or “rim” can be different on each (pair) of faces. The three dimensions of the core of the parallelepiped (strictly here a cuboid) may be given in any size order as long as the particles are randomly oriented (i.e. take on all possible orientations see notes on 2D below). To avoid multiple fit solutions, especially with Monte-Carlo fit methods, it may be advisable to restrict their ranges. There may be a number of closely similar “best fits”, so some trial and error, or fixing of some dimensions at expected values, may help.

The form factor is normalized by the particle volume \(V\) such that

\[I(q) = \frac{\text{scale}}{V} \langle P(q,\alpha,\beta) \rangle + \text{background}\]

where \(\langle \ldots \rangle\) is an average over all possible orientations of the rectangular solid, and the usual \(\Delta \rho^2 \ V^2\) term cannot be pulled out of the form factor term due to the multiple slds in the model.

The core of the solid is defined by the dimensions \(A\), \(B\), \(C\) here shown such that \(A < B < C\).

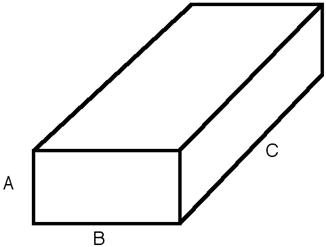
Fig. 60 Core of the core shell parallelepiped with the corresponding definition of sides.

There are rectangular “slabs” of thickness \(t_A\) that add to the \(A\) dimension (on the \(BC\) faces). There are similar slabs on the \(AC\) \((=t_B)\) and \(AB\) \((=t_C)\) faces. The projection in the \(AB\) plane is

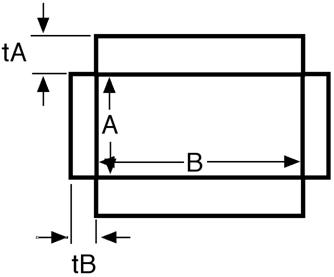
Fig. 61 AB cut through the core-shell parallelipiped showing the cross secion of four of the six shell slabs. As can be seen, this model leaves “gaps” at the corners of the solid.

The total volume of the solid is thus given as

\[V = ABC + 2t_ABC + 2t_BAC + 2t_CAB\]

The intensity calculated follows the parallelepiped model, with the core-shell intensity being calculated as the square of the sum of the amplitudes of the core and the slabs on the edges. The scattering amplitude is computed for a particular orientation of the core-shell parallelepiped with respect to the scattering vector and then averaged over all possible orientations, where \(\alpha\) is the angle between the \(z\) axis and the \(C\) axis of the parallelepiped, and \(\beta\) is the angle between the projection of the particle in the \(xy\) detector plane and the \(y\) axis.

\[P(q)=\frac {\int_{0}^{\pi/2}\int_{0}^{\pi/2}F^2(q,\alpha,\beta) \ sin\alpha \ d\alpha \ d\beta} {\int_{0}^{\pi/2} \ sin\alpha \ d\alpha \ d\beta}\]

and

\[\begin{split}F(q,\alpha,\beta) &= (\rho_\text{core}-\rho_\text{solvent}) S(Q_A, A) S(Q_B, B) S(Q_C, C) \\ &+ (\rho_\text{A}-\rho_\text{solvent}) \left[S(Q_A, A+2t_A) - S(Q_A, A)\right] S(Q_B, B) S(Q_C, C) \\ &+ (\rho_\text{B}-\rho_\text{solvent}) S(Q_A, A) \left[S(Q_B, B+2t_B) - S(Q_B, B)\right] S(Q_C, C) \\ &+ (\rho_\text{C}-\rho_\text{solvent}) S(Q_A, A) S(Q_B, B) \left[S(Q_C, C+2t_C) - S(Q_C, C)\right]\end{split}\]

with

\[S(Q_X, L) = L \frac{\sin (\tfrac{1}{2} Q_X L)}{\tfrac{1}{2} Q_X L}\]

and

\[\begin{split}Q_A &= q \sin\alpha \sin\beta \\ Q_B &= q \sin\alpha \cos\beta \\ Q_C &= q \cos\alpha\end{split}\]

where \(\rho_\text{core}\), \(\rho_\text{A}\), \(\rho_\text{B}\) and \(\rho_\text{C}\) are the scattering lengths of the parallelepiped core, and the rectangular slabs of thickness \(t_A\), \(t_B\) and \(t_C\), respectively. \(\rho_\text{solvent}\) is the scattering length of the solvent.

Note

the code actually implements two substitutions: \(d(cos\alpha)\) is substituted for -\(sin\alpha \ d\alpha\) (note that in the parallelepiped code this is explicitly implemented with \(\sigma = cos\alpha\)), and \(\beta\) is set to \(\beta = u \pi/2\) so that \(du = \pi/2 \ d\beta\). Thus both integrals go from 0 to 1 rather than 0 to \(\pi/2\).

FITTING NOTES

1. There are many parameters in this model. Hold as many fixed as possible with known values, or you will certainly end up at a solution that is unphysical.

2. The 2nd virial coefficient of the core_shell_parallelepiped is calculated based on the the averaged effective radius \((=\sqrt{(A+2t_A)(B+2t_B)/\pi})\) and length \((C+2t_C)\) values, after appropriately sorting the three dimensions to give an oblate or prolate particle, to give an effective radius for \(S(q)\) when \(P(q) * S(q)\) is applied.

3. For 2d data the orientation of the particle is required, described using angles \(\theta\), \(\phi\) and \(\Psi\) as in the diagrams below, where \(\theta\) and \(\phi\) define the orientation of the director in the laboratory reference frame of the beam direction (\(z\)) and detector plane (\(x-y\) plane), while the angle \(\Psi\) is effectively the rotational angle around the particle \(C\) axis. For \(\theta = 0\) and \(\phi = 0\), \(\Psi = 0\) corresponds to the \(B\) axis oriented parallel to the y-axis of the detector with \(A\) along the x-axis. For other \(\theta\), \(\phi\) values, the order of rotations matters. In particular, the parallelepiped must first be rotated \(\theta\) degrees in the \(x-z\) plane before rotating \(\phi\) degrees around the \(z\) axis (in the \(x-y\) plane). Applying orientational distribution to the particle orientation (i.e jitter to one or more of these angles) can get more confusing as jitter is defined NOT with respect to the laboratory frame but the particle reference frame. It is thus highly recommended to read Oriented Particles for further details of the calculation and angular dispersions.

Note

For 2d, constraints must be applied during fitting to ensure that the order of sides chosen is not altered, and hence that the correct definition of angles is preserved. For the default choice shown here, that means ensuring that the inequality \(A < B < C\) is not violated, The calculation will not report an error, but the results may be not correct.

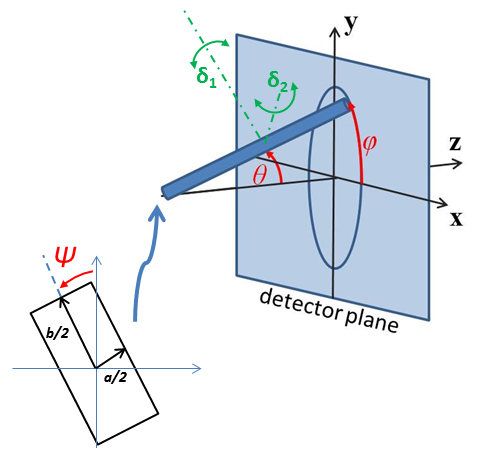
Fig. 62 Definition of the angles for oriented core-shell parallelepipeds. Note that rotation \(\theta\), initially in the \(x-z\) plane, is carried out first, then rotation \(\phi\) about the \(z\) axis, finally rotation \(\Psi\) is now around the \(C\) axis of the particle. The neutron or X-ray beam is along the \(z\) axis and the detecotr defines the \(x-y\) plane.

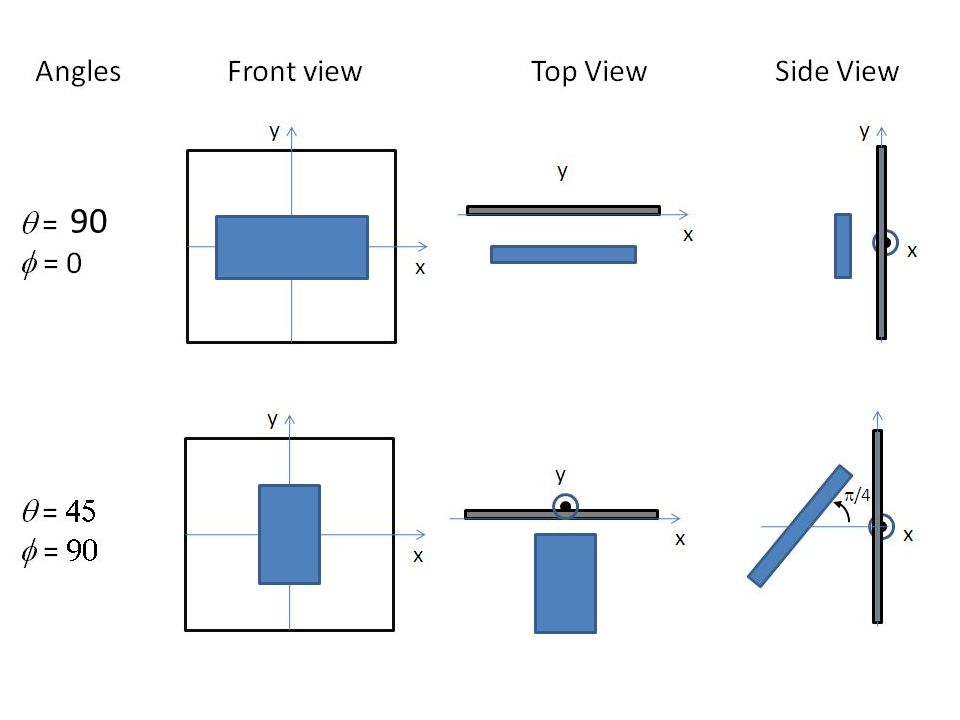
Fig. 63 Examples of the angles for oriented core-shell parallelepipeds against the detector plane.

Validation

Cross-checked against hollow rectangular prism and rectangular prism for equal thickness overlapping sides, and by Monte Carlo sampling of points within the shape for non-uniform, non-overlapping sides.

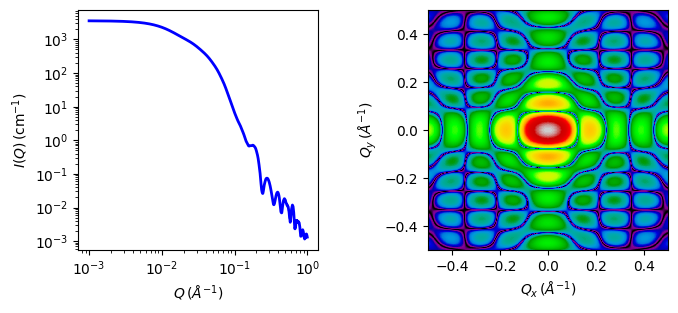
Fig. 64 1D and 2D plots corresponding to the default parameters of the model.

Source

core_shell_parallelepiped.py \(\ \star\ \) core_shell_parallelepiped.c \(\ \star\ \) gauss76.c

References

1. P Mittelbach and G Porod, Acta Physica Austriaca, 14 (1961) 185-211 Equations (1), (13-14). (in German)

2. D Singh (2009). Small angle scattering studies of self assembly in lipid mixtures, Johns Hopkins University Thesis (2009) 223-225. Available from Proquest

3. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Converted to sasmodels by: Miguel Gonzalez Date: February 26, 2016

• Last Modified by: Paul Kienzle Date: October 17, 2017

• Last Reviewed by: Paul Butler Date: May 24, 2018 - documentation updated