pringle

The Pringle model provides the form factor, $P(q)$, for a ‘pringle’ or ‘saddle-shaped’ disc that is bent in two directions.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
radius	Pringle radius	Å	60
thickness	Thickness of pringle	Å	10
alpha	Curvature parameter alpha	None	0.001
beta	Curvature paramter beta	None	0.02
sld	Pringle sld	10-6Å-2	1
sld_solvent	Solvent sld	10-6Å-2	6.3

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

The form factor for this bent disc is essentially that of a hyperbolic paraboloid and calculated as

$$P(q) = (\Delta \rho )^2 V \int^{\pi/2}_0 d\psi \sin{\psi} sinc^2 \left( \frac{qd\cos{\psi}}{2} \right) \left[ \left( S^2_0+C^2_0\right) + 2\sum_{n=1}^{\infty} \left( S^2_n+C^2_n\right) \right]$$

where

$$C_n = \frac{1}{r^2}\int^{R}_{0} r dr\cos(qr^2\alpha \cos{\psi}) J_n\left( qr^2\beta \cos{\psi}\right) J_{2n}\left( qr \sin{\psi}\right)$$

$$S_n = \frac{1}{r^2}\int^{R}_{0} r dr\sin(qr^2\alpha \cos{\psi}) J_n\left( qr^2\beta \cos{\psi}\right) J_{2n}\left( qr \sin{\psi}\right)$$

and $\Delta\rho\text{ is }\rho_{pringle}-\rho_{solvent}$, $V$ is the volume of the disc, $\psi$ is the angle between the normal to the disc and the q vector, $d$ and $R$ are the “pringle” thickness and radius respectively, $\alpha$ and $\beta$ are the two curvature parameters, and $J_n$ is the n^th order Bessel function of the first kind.

Fig. 34 Schematic of model shape (Graphic from Matt Henderson, matt@matthen.com)

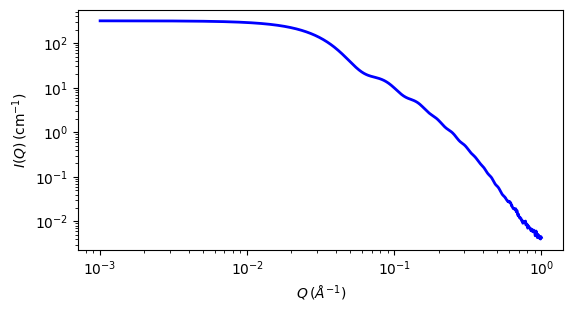
Fig. 35 1D plot corresponding to the default parameters of the model.

Source

pringle.py $\ \star\ $ pringle.c $\ \star\ $ gauss76.c $\ \star\ $ sas_JN.c $\ \star\ $ sas_J1.c $\ \star\ $ sas_J0.c $\ \star\ $ polevl.c

Reference

1. Karen Edler, Universtiy of Bath, Private Communication. 2012. Derivation by Stefan Alexandru Rautu.

2. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author: Andrew Jackson Date: 2008

• Last Modified by: Wojciech Wpotrzebowski Date: March 20, 2016

• Last Reviewed by: Andrew Jackson Date: September 26, 2016