surface_fractal

Fractal-like aggregates based on the Mildner reference

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
radius	Particle radius	Å	10
fractal_dim_surf	Surface fractal dimension	None	2
cutoff_length	Cut-off Length	Å	500

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model calculates the scattering from fractal-like aggregates based on the Mildner reference.

Definition

The scattering intensity \(I(q)\) is calculated as

\begin{align*} I(q) &= \text{scale} \times P(q)S(q) + \text{background} \\ P(q) &= F(qR)^2 \\ F(x) &= \frac{3\left[\sin(x)-x\cos(x)\right]}{x^3} \\ S(q) &= \Gamma(5-D_S)\xi^{\,5-D_S}\left[1+(q\xi)^2 \right]^{-(5-D_S)/2} \sin\left[-(5-D_S) \tan^{-1}(q\xi) \right] q^{-1} \\ \text{scale} &= \text{scale factor}\, N V^1(\rho_\text{particle} - \rho_\text{solvent})^2 \\ V &= \frac{4}{3}\pi R^3 \end{align*}

where \(R\) is the radius of the building block, \(D_S\) is the surface fractal dimension, \(\xi\) is the cut-off length, \(\rho_\text{solvent}\) is the scattering length density of the solvent and \(\rho_\text{particle}\) is the scattering length density of particles.

Note

The surface fractal dimension is only valid if \(1<D_S<3\). The result is only valid over a limited \(q\) range, \(\tfrac{5}{3-D_S}\xi^{\,-1} < q < R^{-1}\). See the reference for details.

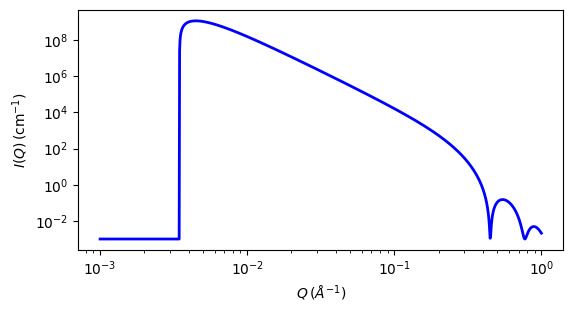
Fig. 124 1D plot corresponding to the default parameters of the model.

Source

surface_fractal.py \(\ \star\ \) surface_fractal.c \(\ \star\ \) sas_gamma.c \(\ \star\ \) sas_3j1x_x.c

References

1. D Mildner and P Hall, J. Phys. D: Appl. Phys., 19 (1986) 1535-1545

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: