elliptical_cylinder

Form factor for an elliptical cylinder.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
radius_minor	Ellipse minor radius	Å	20
axis_ratio	Ratio of major radius over minor radius	None	1.5
length	Length of the cylinder	Å	400
sld	Cylinder scattering length density	10-6Å-2	4
sld_solvent	Solvent scattering length density	10-6Å-2	1
theta	cylinder axis to beam angle	degree	90
phi	rotation about beam	degree	0
psi	rotation about cylinder axis	degree	0

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

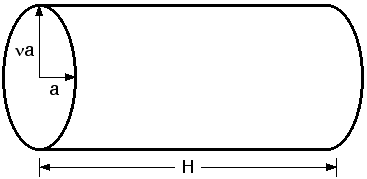
Fig. 24 Elliptical cylinder geometry \(a = r_\text{minor}\) and \(\nu = r_\text{major} / r_\text{minor}\) is the axis_ratio.

The function calculated is

\[I(\vec q)=\frac{1}{V_\text{cyl}}\int{d\psi}\int{d\phi}\int{ p(\theta,\phi,\psi)F^2(\vec q,\alpha,\psi)\sin(\alpha)d\alpha}\]

with the functions

\[F(q,\alpha,\psi) = 2\frac{J_1(a)\sin(b)}{ab}\]

where

\[ \begin{align}\begin{aligned}a = qr'\sin(\alpha)\\b = q\frac{L}{2}\cos(\alpha)\\r'=\frac{r_{minor}}{\sqrt{2}}\sqrt{(1+\nu^{2}) + (1-\nu^{2})cos(\psi)}\end{aligned}\end{align} \]

and the angle \(\psi\) is defined as the orientation of the major axis of the ellipse with respect to the vector \(\vec q\). The angle \(\alpha\) is the angle between the axis of the cylinder and \(\vec q\).

For 1D scattering, with no preferred orientation, the form factor is averaged over all possible orientations and normalized by the particle volume

\[P(q) = \text{scale} <F^2> / V\]

For 2d data the orientation of the particle is required, described using a different set of angles as in the diagrams below, for further details of the calculation and angular dispersions see Oriented Particles.

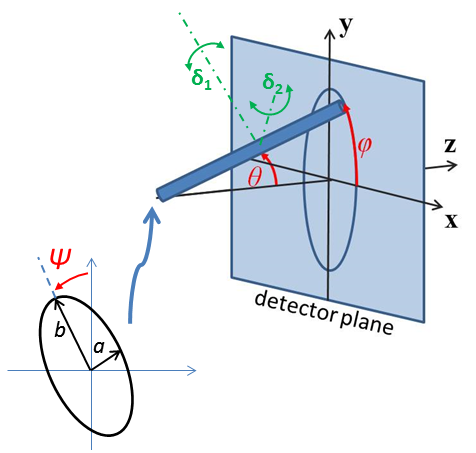
Fig. 25 Note that the angles here are not the same as in the equations for the scattering function. Rotation \(\theta\), initially in the \(xz\) plane, is carried out first, then rotation \(\phi\) about the \(z\) axis, finally rotation \(\Psi\) is now around the axis of the cylinder. The neutron or X-ray beam is along the \(z\) axis.

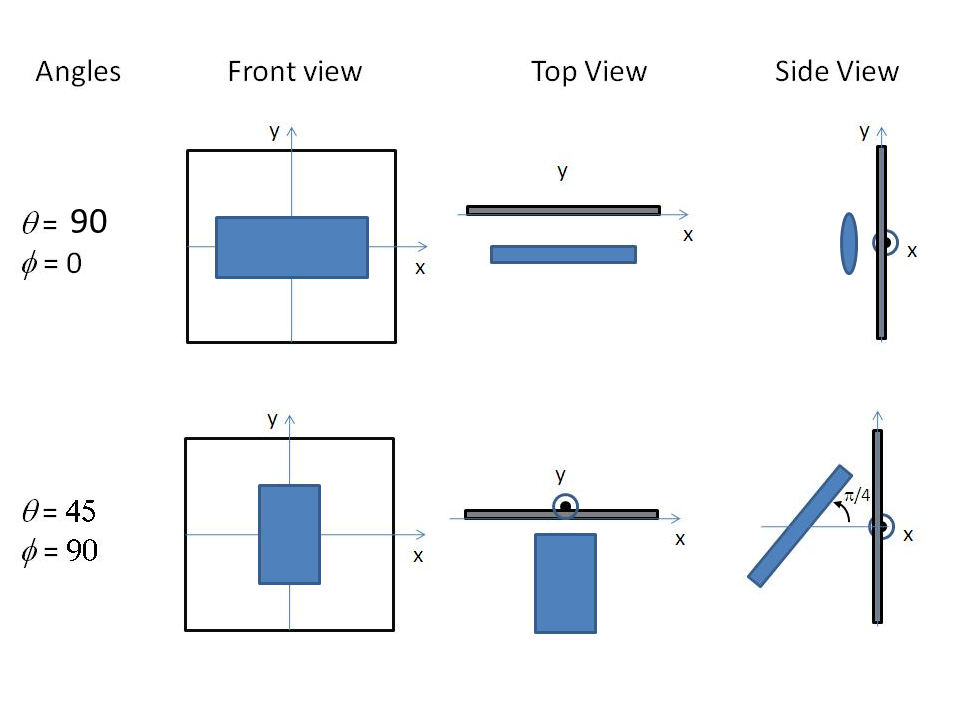
Fig. 26 Examples of the angles for oriented elliptical cylinders against the detector plane, with \(\Psi\) = 0.

The \(\theta\) and \(\phi\) parameters to orient the cylinder only appear in the model when fitting 2d data.

NB: The 2nd virial coefficient of the cylinder is calculated based on the averaged radius \((=\sqrt{r_\text{minor}^2 * \text{axis ratio}})\) and length values, and used as the effective radius for \(S(Q)\) when \(P(Q)*S(Q)\) is applied.

Validation

Validation of our code was done by comparing the output of the 1D calculation to the angular average of the output of the 2D calculation over all possible angles.

In the 2D average, more binning in the angle \(\phi\) is necessary to get the proper result. The following figure shows the results of the averaging by varying the number of angular bins.

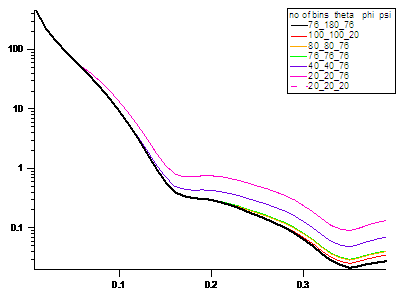
Fig. 27 The intensities averaged from 2D over different numbers of bins and angles.

Fig. 28 1D and 2D plots corresponding to the default parameters of the model.

Source

elliptical_cylinder.py \(\ \star\ \) elliptical_cylinder.c \(\ \star\ \) gauss76.c \(\ \star\ \) sas_J1.c \(\ \star\ \) polevl.c

References

1. L A Feigin and D I Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum, New York, (1987) [see table 3.4]

2. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: Richard Heenan - corrected equation in docs Date: December 21, 2016