flexible_cylinder

Flexible cylinder where the form factor is normalized by the volume of the cylinder.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
length	Length of the flexible cylinder	Å	1000
kuhn_length	Kuhn length of the flexible cylinder	Å	100
radius	Radius of the flexible cylinder	Å	20
sld	Cylinder scattering length density	10-6Å-2	1
sld_solvent	Solvent scattering length density	10-6Å-2	6.3

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model provides the form factor, \(P(q)\), for a flexible cylinder where the form factor is normalized by the volume of the cylinder. Inter-cylinder interactions are NOT provided for.

\[P(q) = \text{scale} \left<F^2\right>/V + \text{background}\]

where the averaging \(\left<\ldots\right>\) is applied only for the 1D calculation

The 2D scattering intensity is the same as 1D, regardless of the orientation of the q vector which is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]

Definitions

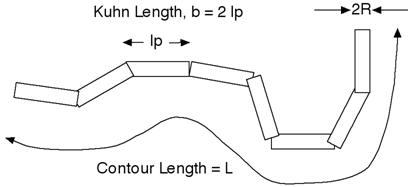
The chain of contour length, \(L\), (the total length) can be described as a chain of some number of locally stiff segments of length \(l_p\), the persistence length (the length along the cylinder over which the flexible cylinder can be considered a rigid rod). The Kuhn length \((b = 2*l_p)\) is also used to describe the stiffness of a chain.

In the parameters, the sld and sld_solvent represent the SLD of the cylinder and solvent respectively.

Our model uses the form factor calculations in reference [1] as implemented in a c-library provided by the NIST Center for Neutron Research (Kline, 2006). This states:

‘Method 3 With Excluded Volume’ is used. The model is a parametrization of simulations of a discrete representation of the worm-like chain model of Kratky and Porod applied in the pseudocontinuous limit. See equations (13,26-27) in the original reference for the details.

Note

There are several typos in the original reference that have been corrected by Chen et al (WRC) [2]. Details of the corrections are in the reference below. Most notably

• Equation (13): the term \((1 - w(QR))\) should swap position with \(w(QR)\)

• Equations (23) and (24) are incorrect; WRC has entered these into Mathematica and solved analytically. The results were then converted to code.

• Equation (27) should be \(q0 = max(a3/(Rg^2)^{1/2},3)\) instead of \(max(a3*b(Rg^2)^{1/2},3)\)

• The scattering function is negative for a range of parameter values and q-values that are experimentally accessible. A correction function has been added to give the proper behavior.

This is a model with complex behaviour depending on the ratio of \(L/b\) and the reader is strongly encouraged to read reference [1] before use. In particular, the cylinder form factor used as the limiting case for long narrow rods will not be exactly correct for short and/or wide rods.

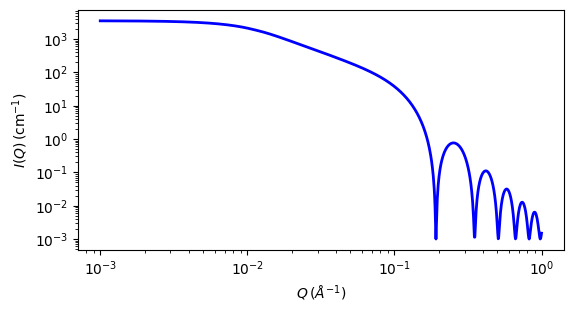
Fig. 29 1D plot corresponding to the default parameters of the model.

Source

flexible_cylinder.py \(\ \star\ \) flexible_cylinder.c \(\ \star\ \) wrc_cyl.c \(\ \star\ \) sas_J1.c \(\ \star\ \) polevl.c

References

1. J S Pedersen and P Schurtenberger. Scattering functions of semiflexible polymers with and without excluded volume effects. Macromolecules, 29 (1996) 7602-7612

2. W R Chen, P D Butler and L J Magid, Incorporating Intermicellar Interactions in the Fitting of SANS Data from Cationic Wormlike Micelles. Langmuir, 22(15) 2006 6539-6548

Authorship and Verification

• Author:

• Last Modified by:

• Last Reviewed by: Steve King Date: March 6, 2020