sphere

Spheres with uniform scattering length density

Parameter

Description

Units

Default value

scale

Scale factor or Volume fraction

None

1

background

Source background

cm-1

0.001

sld

Layer scattering length density

10-6Å-2

1

sld_solvent

Solvent scattering length density

10-6Å-2

6

radius

Sphere radius

Å

50

The returned value is scaled to units of cm-1 sr-1, absolute scale.

For information about polarised and magnetic scattering, see the Polarisation/Magnetic Scattering documentation.

Definition

The 1D scattering intensity is calculated in the following way (Guinier, 1955)

\[I(q) = \frac{\text{scale}}{V} \cdot \left[ 3V(\Delta\rho) \cdot \frac{\sin(qr) - qr\cos(qr))}{(qr)^3} \right]^2 + \text{background}\]

where scale is a volume fraction, \(V\) is the volume of the scatterer, \(r\) is the radius of the sphere and background is the background level. sld and sld_solvent are the scattering length densities (SLDs) of the scatterer and the solvent respectively, whose difference is \(\Delta\rho\).

Note that if your data is in absolute scale, the scale should represent the volume fraction (which is unitless) if you have a good fit. If not, it should represent the volume fraction times a factor (by which your data might need to be rescaled).

The 2D scattering intensity is the same as above, regardless of the orientation of \(\vec q\).

Validation

Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006).

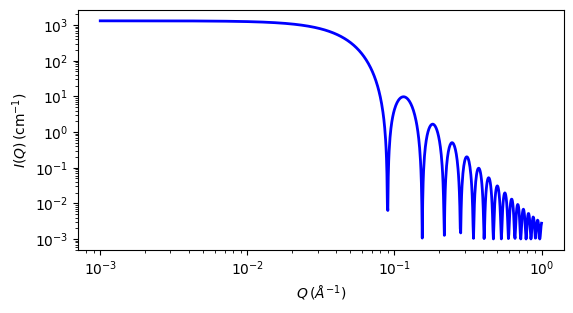
../../_images/sphere_autogenfig.png

Fig. 92 1D plot corresponding to the default parameters of the model.

Source

sphere.py \(\ \star\ \) sphere.c \(\ \star\ \) sas_3j1x_x.c

References

  1. A Guinier and G. Fournet, Small-Angle Scattering of X-Rays, John Wiley and Sons, New York, (1955)

Authorship and Verification

  • Author:

  • Last Modified by:

  • Last Reviewed by: S King and P Parker Date: 2013/09/09 and 2014/01/06