Generic SAS Calculator Tool¶

Description¶

This tool calculates the small angle scattering cross-section expected from a given real-space 3D shape/structure. The tool can handle both nuclear and magnetic contributions to the scattering. It is found selecting Tool>Generic Scattering Calculator from the top menu.

This documentation begins by briefly covering the two main data structures which can be used by the calculator, followed by an overview of the three different coordinate systems used to orient the data and beamline parameters. For those unfamiliar with magnetic scattering a link to the Polarisation/Magnetic Scattering documentation is also provided.

Next the interface to the calculator is covered, with details of each of the settings; both the various inputs to the calculator, and the information panels. Finally a description of the various file types which can be used to store sample data is given.

For those who wish to use the calculator in more advanced ways a brief overview of the scripting interface follows, before the documentation concludes with links to some examples and the references.

Data Structure¶

The calculator processes data with the following structure: either rectangular pixels (grid type data), or finite elements (element type data), in a variety of shapes, such as tetrahedra, cubes or hexahedra.

The scattering length density (SLD) is assumed uniform for each pixel or element. Depending on the data format the property is either nuclear (in units of Å^-2) (PDB file) or magnetic SLDs (OMF file) or a combination of both (SLD and VTK files). For magnetic neutron scattering, the Polarisation/Magnetic Scattering documentation gives further details and describes how to construct the various neutron spin resolved scattering cross section.

Grid Type Data¶

In the simplest case, a space (simulation box) with volume \(V\) can be discretized with \(N\) 3-dimensional rectangular pixels.

The elastic scattering intensity is defined as

\[I(\mathbf{Q}) = \frac{1}{V}\left\lvert\sum_j^Nv_j\rho_j\exp(i\mathbf{Q}\cdot\mathbf{r_j})\right\rvert^2\]

where \(\rho_j\) and \(\mathbf{r}_j\) are the scattering length density and the position of the \(j^\text{th}\) pixel respectively.

The total volume \(V_s\) of structures different than the homogenous media is equal to

\[V_s = \sum_j^N v_j\]

for \(\rho_j \ne 0\) where \(v_j\) is the volume of the \(j^\text{th}\) pixel or natural atomic volume (for .pdb). For atomic structures \(v_j \rho_j \equiv b_j\) is the scattering length of the \(j^\text{th}\) atom and the natural atomic volume is given by:

\(\frac{\text{atomic mass}}{\text{natural molar density}\times\text{Avogadro number}}\)

\(V_s\) can be corrected by users (input parameter Total volume). This correction is useful especially for an atomic structure (such as taken from a PDB file) to get the right normalization.

For non-magnetic, grid-type data the 1D orientationally averaged scatting intensity profile can also be calculated using the Debye full average option which uses the Debye formula:

\[I(\left\lvert\mathbf{Q}\right\rvert) = \frac{1}{V}\sum_j^N v_j\rho_j \sum_k^N v_k\rho_k \frac{\sin\left(\left\lvert\mathbf{Q}\right\rvert\left\lvert\mathbf{r_j}-\mathbf{r_k}\right\rvert\right)} {\left\lvert\mathbf{Q}\right\rvert\left\lvert\mathbf{r_j}-\mathbf{r_k}\right\rvert}\]

NOTE: \(\rho_j\) displayed in the GUI may be incorrect (input parameter solvent_SLD ) but this will not affect the scattering computation if the correction of the total volume V is made.

Element Type Data¶

The simulation box can be described as collection of finite elements forming a mesh. For example this cube is formed of five finite elements:

Each element has an associated scattering length density (\(\rho_j\)) for the occupied space \(V_j\) and the elastic scattering intensity is calculated as

\[I(\mathbf{Q}) = \frac{1}{V}\left\lvert\sum_j^N\rho_j\iiint\limits_{V_j}\exp(i\mathbf{Q}\cdot\mathbf{r_j})\text{d}V\right\rvert^2\]

Note that the Fourier transform is calculated over each element - allowing regions of space with little variation in \(\rho\) to have larger finite elements, and regions of interest to have much smaller finite elements, and hence more detail.

In Sasview an algorithm is implemented to calculate the Fourier transform over polygons utilizing the divergence theorem as described in Maranville [1]

Coordinate Systems¶

The general scattering calculator offers 3 different coordinate systems to enable any orientation of the sample, the magnetic field and polarisation, as well as the surrounding sample environment with respect to the instrument reference frame:

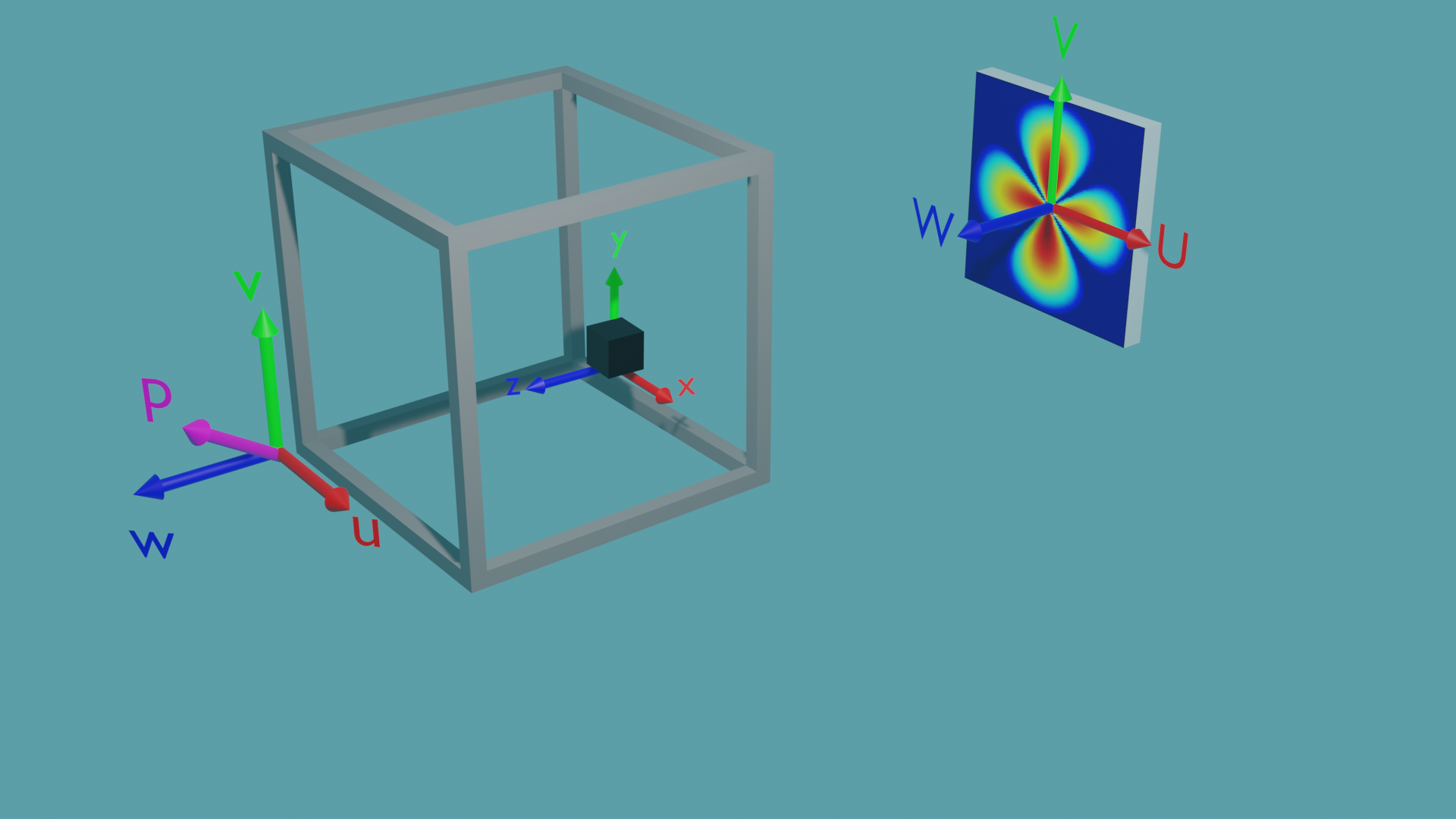
The \({U,V,W}\) coordinates are the beamline coordinates - they define the coordinate system of the target and source. The Qx and Qy coordinates of the detector align with the \(U\) and \(V\) axes, and the \(W\) axis points back to the source.

The \({u,v,w}\) coordinates are the environment coordinates - they define the coordinate system of the sample environment - such as the cryostat. In this coordinate system is also the neutron polarisation vector \(\mathbf{P}\) located which is given by the applied magnetic field. The orientation of \(\mathbf{P}\) is set with the values up_theta and up_phi, where up_theta is the polar angle from the \(w\) axis to the \(u\)-\(v\) plane, and up_phi is the azimuthal angle directed anticlockwise in the \(u\)-\(v\) plane from the positive \(u\) axis.

The \({x,y,z}\) coordinates are the sample coordinates - they define the position vectors and magnetisation vectors of individual pixels or elements in the sample.

Within the generic scattering calculator all three coordinate systems are initially aligned. By altering the yaw, pitch and roll values their relative rotations can be set. The environment is rotated relative to the beamline, and the sample is rotated relative to the environment. The rotations are carried out in the order yaw, pitch then roll, intrinsically. For example when rotating the environment coordinates relative to the beamline:

the \({u,v,w}\) and \({U,V,W}\) coordinates are initially aligned

a rotation of angle yaw about the \(V\) axis takes \({U,V,W} \rightarrow {U',V',W'}\)

a rotation of angle pitch about the \(U'\) axis takes \({U',V',W'} \rightarrow {U'',V'',W''}\)

a rotation of angle roll about the \(W''\) axis takes \({U'',V'',W''} \rightarrow {u,v,w}\)

Magnetic Scattering¶

For more information about polarised and magnetic scattering, see the Polarisation/Magnetic Scattering documentation.

How to use the Tool¶

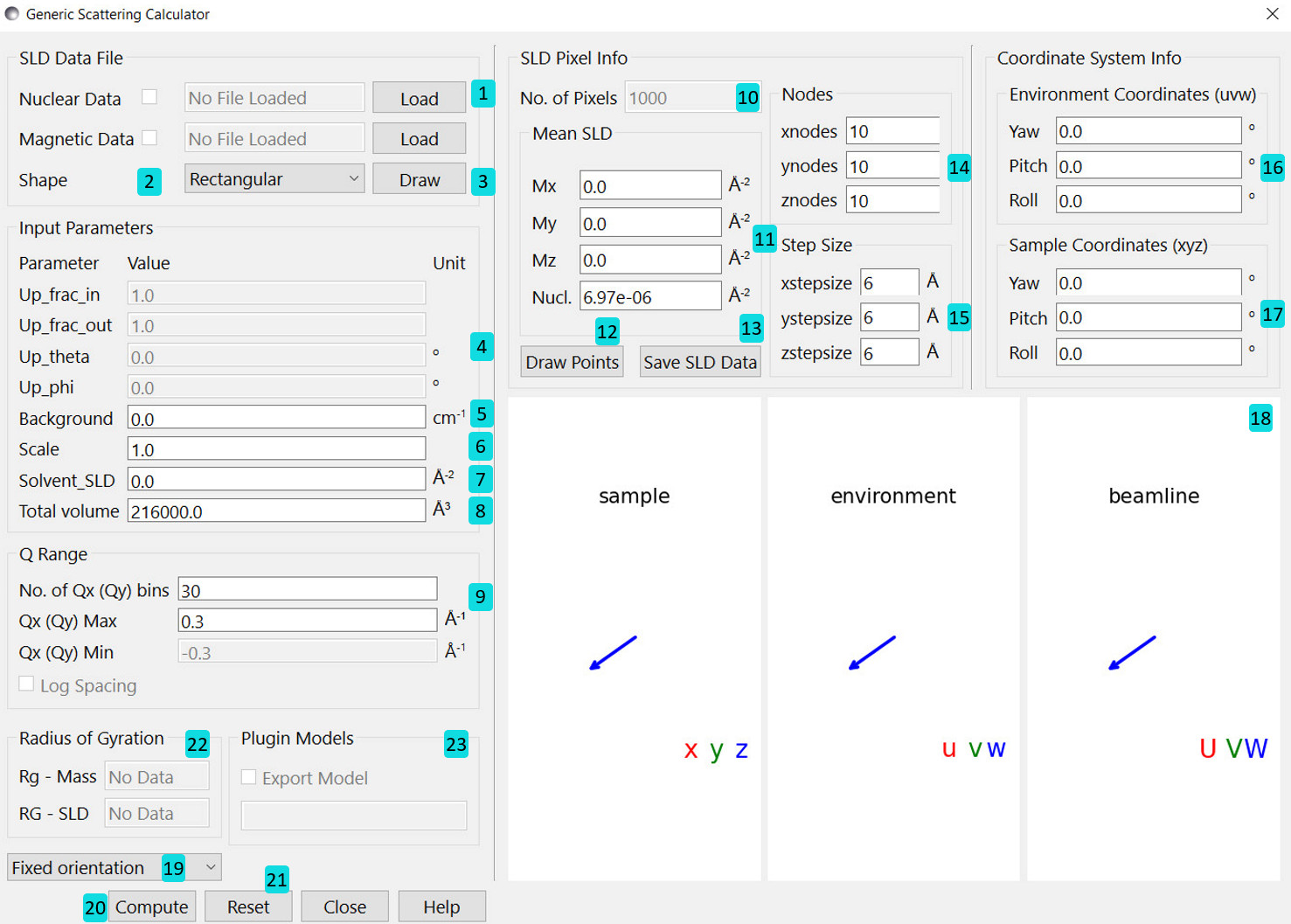
Upon loading the calculator we are shown the following interface:

../../../_images/GSC_Oct282023_GUI_Index2.jpg

Inputs¶

Load .sld, .pdb, .omf or .vtk datafile. Further description of each file type can be found here. The program can hold up to two files - one to describe the nuclear SLDs and one for magnetic SLDs. The checkboxes enable or disable a loaded file. If both files are enabled they must describe the same pixels/elements in real space. The program can only verify that congruent data set are loaded. It is up to you to check that structural and magnetic data match and describe the same scenario.

Select the default shape of a sample. Mostly interesting for testing purposes.

Draw structure and magnetisation with arrows (not recommended for a large number of pixels/elements). Pixels with zero valued SLD will appear yellow.

Variables describing the instrument setup for polarisation. These options are only enabled when magnetic SLDs are non-zero - otherwise they have no effect.

up_frac_in describes the neutron spin state before the sample.

up_frac_out describes the neutron spin state after the analyser.

Up_frac_in and Up_frac_out are the ratio \(\frac{\text{spin up}}{\text{spin up} + \text{spin down}}\). The values of up_frac_in and up_frac_out must be in the range 0.0 to 1.0, 0 denotes a “+” state, and 1 the opposite “-” state as defined in Moon, Riste, and Koehler, 1969 [2]. An unpolarized neutron beam is associated to a value of 0.5.

up_theta is the polar angle of the polarisation in degrees from the \(w\) axis to the \(u\)-\(v\) plane.

up_phi is the azimuthal angle of the polarisation in degrees around the \(u\)-\(v\) plane. The coordinate systems of the scattering calculator are described above.

The background intensity of the detector.

A relative scaling factor for the output intensity.

The SLD of the solvent for the sample.

The default volume calculated from the pixel info (or natural density of PDB file).

Set the resolution of the scattering pattern.

No. of Qx (Qy) bins determines the number of evenly spaced \(Q\) bins on each axis.

Qx (Qy) Max is the maximum momentum transfer on each axis. In some circumstances these textboxes will be highlighted orange, as a warning that with the values chosen numerical artefacts may appear due to the Nyquist criterion, or simulation box size.

When calculating 1D data, Q values are evenly spaced in the log scale if “Log Spacing” box is checked.

Information Panel¶

The number of pixels/elements loaded.

The mean SLD, both nuclear SLD and all 3 components of the magnetic SLD. If a nuclear/magnetic file is enabled then the nuclear/magnetic SLD textboxes are read only. If no file is enabled then the respective textboxes can be edited - and the value supplied is taken to be a constant across all pixels/elements.

Draw the pixels/atoms without magnetisation arrows.

Save the current data into a SLD file. This combines the currently enabled files with any values altered in the GUI, and saves it to a file for later reuse. This functionality only works with grid type data.

For grid type data these values specify the number of pixels in the \(x\), \(y\) and \(z\) directions respectively.

For grid type data these values specify the spacing between pixels in the \(x\), \(y\) and \(z\) directions.

These variables define the yaw, pitch and roll rotation of the environment coordinates relative to the beamline coordinates (see coordinate description above).

These variables define the yaw, pitch and roll rotation of the sample coordinates relative to the environment coordinates (see coordinate description above).

The 3D display shows the relative orientation of the three different coordinate systems, with a grey square representing the beamline detector. When magnetic SLDs are present a polarisation vector \(\mathbf{P}\) is also shown in the environment coordinates. The display can be dragged around with the mouse, and the mousewheel used to zoom in and out.

This choice appears only for grid type data and without magnetic SLD. This tool allows to either compute the fully oriented 2D scattering pattern, or calculating the 1D orientational averaged intensity \(I(Q)\) by the Debye equation. One can also choose a compuation option, Debye full avg. w/ \(\beta(Q)\), to calculate 1D scattering pattern together with \(\beta(Q)\). \(\beta(Q)\) is needed when fitting scattering patterns of concentrated solutions using the inter-particle structure factor, \(S(Q)\), with the static decoupling approximation.

Starts the computation of the scattering pattern.

Reset GUI to the initial state.

If a PDB file is loaded, the radius of gyration is calculated and displayed. “Rg-MASS” is the radius of gyration based on the mass of all atoms in a molecule. “RG-SLD” is the radius of gyration based on the scattering length of all atoms.

If the option, Debye full avg. w/ \(\beta(Q)\), is chosen, one has the option to check the box “Export Model”. Once checked, one can input a file name in the box below. During the computation, the program then exports the calculated normalized form factor, \(P(Q)\), and \(\beta(Q)\) into this file that automatically become a model in the “Plugin Models”. The model name is the same as the file name given in the blox below “Export Model”.

One example is given here ( Click here ) to illustrate how to calculate \(P(Q)\) and \(\beta(Q)\) using a PDB file of a protein. These are 1D functions after averaging over all orientiations of proteins. The program can generate a custom model function, which can be used to fit the 1D small angle scattering data.

One other example ( Click here ) is a simple demonstration of the functionality of the Generic scattering calculator to calculate the 2D scattering pattern using the default starting values with no files loaded.

After computation the result will appear in the Data Explorer panel and can be used further just as any data set in Sasview for further analysis.

NOTE: An imaginary nuclear SLD indicates a bound neutron state. That means the neutron will be either absorbed by an atom (potentially producing some nuclear decay). If in any case some neutron is re-emitted, it will happen in a more or less arbitrary direction. This is the reason for the large incoherent neutron scattering background with hydrogenous materials.

File Types¶

SLD Files¶

An SLD file is a text file format capable of storing grid type data with both nuclear and magnetic SLDs. The file format for an SLD file is as follows:

One line of header information - this is unused by the program and can contain any information

\(N\) lines describing \(N\) pixels, of 4, 6, 7 or 8 columns, separated by whitespace. All lines must have the same number of columns, and the data in each column must be castable to a float.

4 columns describe x position, y position, z position, nuclear SLD

6 columns describe x position, y position, z position, magnetic SLD (x, y, z components)

7 columns describe x position, y position, z position, nuclear SLD, magnetic SLD (x, y, z components)

8 columns describe x position, y position, z position, nuclear SLD, magnetic SLD (x, y, z components), pixel volume

The file specification does not guarantee that the pixels form a rectangular grid - however this is required for the output of the scattering calculator to be correct. The program does NOT check this.

PDB Files¶

A Protein Data Bank (PDB) file is a text file format which can store atomic structure data. The specification is given here. This format is read as grid type data and can be used to create nuclear SLDs only.

Note that Sasview only reads ATOM and CONECT records from these files. ATOM records are used to create suitable nuclear SLDs and pixel volumes using data from the periodictable Python package. CONECT records are only used when drawing the structure.

OMF Files¶

The file format OMF is designated to store spatial magnetisation vector fields. The specification can be found here. While the OVF 2.0 format could technically also store both nuclear and magnetic SLD data, Sasview currently reads all OMF files as if they were OVF 1.0 or lower, and as such OMF files can only be used to read in data to create magnetic SLDs. Unlike SLD files, OMF files are expected to store the magnetisation vector \(\mathbf{M}\), not the magnetic SLD. Sasview will calculate the corresponding magnetic SLD based on the magnetisation unit provided with the OMF file.

While there is no explicit check within the program only OMF files with meshtype: rectangular can be read into the program correctly. Additionally the data must be stored as ‘Text’ (ASCII format), Sasview cannot read in binary data.

VTK Files¶

The VTK file format is a very broad set of file formats, specifically Sasview currently reads in “legacy” .vtk files, up to version 3.0. The file specification is available here. Currently Sasview only reads in the ‘unstructured grid’ dataset format, and while any file of this form can be loaded, only files in which all cells are of the same type (type=10 (tetrahedron), 11 (voxel), 12 (hexahedron)) can be used to compute scattering patterns. While this may seem restrictive it merely requires that every element has the same number of faces, and every face the same number of vertices.

VTK files are treated as element type data - and can contain magnetic and/or nuclear SLDs. The nuclear SLD is identified with a set of SCALAR data with one component. The magnetic SLD is identified with a set of SCALAR data with three components or as a set of VECTOR data. If the data is provided to the points of the mesh and not the cells, a weighted average is taken to find an estimate for the SLD at the centre of each element. This weighted average is given by:

\[\bar{\rho} = \frac{\sum\limits_j^n \rho_j r_j^{\prime -2}}{\sum\limits_j^nr_j^{\prime -2}}\]

Where \(\bar{\rho}\) is the estimated SLD for an element and \(\rho_j\), \(r'_j\) are the SLDs and distances from the centre of the element of each of the \(n\) vertices of the element respectively. \(r'_j\) is taken as:

\[r^\prime_j = \left\lvert \mathbf{r_j} - \frac{1}{n}\sum_k^n \mathbf{r_k}\right\rvert\]

where \(\mathbf{r_k}\) are the position vectors of the n vertices of the element.

Scripting¶

For more advanced uses the GUI version of the scattering calculator may not suffice or can be very cumbersome without scripting, for example the orientational average of a magnetic structure, or rocking scans around specific sample axis. For full details of the Python scripting interface please see the developer documentation: sas.sascalc.calculator.sas_gen(). A short introduction is provided here to the most useful elements of the general scattering calculator interface.

To begin a Python script we import the sas_gen module of Sasview. If the location of this module is unknown to python, it can be imported with:

import sys
sys.path.append("filepath to sasview/src")
from sas.sascalc.calculator import sas_gen

If Python does know the location of the Sasview installation only the final line is necessary.

The sas_gen module contains several useful classes for reading and processing data. The most important of these are:

GenSAS: This class provides the actual interface to the calculation of scattering patterns. It stores all the required data and parameters, and has methods which can return scattering intensities. It will be referred to hereafter also as ‘the model’, since it is the overarching object which models the scattering.

MagSLD: This class stores all the data associated with a sample, such as scattering length densities. An instance of this class is provided to the model to set the sample data.

OMFData: This class stores sample data from OMF files. It is converted via an OMF2SLD object into a MagSLD object before it can be used by the model.

VTKReader: This class reads in legacy VTK files and returns a MagSLD object with the associated data.

PDBReader: This class reads in PDB files and returns a MagSLD object with the associated data.

SLDReader: This class reads in SLD files and returns a MagSLD object with the associated data.

OMFReader: This class reads in OMF files and returns a OMFData object with the associated data.

The general stages in a script are:

Create a MagSLD object storing the sample data, either programmatically or by loading in a file.

Create a GenSAS model, load in the data, and set the parameters along with any relevant information about the coordinate systems used.

Generate the scattering intensity data from the model and display/process/save it.

1) Data creation¶

Loading data from VTK, PDB or SLD files is easily done with:

vtkloader = sas_gen.VTKReader()
vtkData = vtkloader.read("filepath to vtk file") # a MagSLD object

pdbloader = sas_gen.PDBReader()
pdbData = pdbloader.read("filepath to pdb file") # a MagSLD object

sldloader = sas_gen.SLDReader()
sldData = sldloader.read("filepath to sld file") # a MagSLD object

Loading data from OMF files requires an extra conversion step:

omfloader = sas_gen.OMFReader()
omfIntermediateData = omfloader.read("filepath to omf file") # an OMFData object
omfConverter = sas_gen.OMF2SLD()
omfConverter.set_data(omfIntermediateData)
omfData = OMFConverter.get_output() # a MagSLD object

Alternatively, a MagSLD object can be directly created with custom data, which may have been generated programmatically. The MagSLD object can be created with the following constructor:

def __init__(self, pos_x, pos_y, pos_z, sld_n=None, sld_mx=None, sld_my=None, sld_mz=None, vol_pix=None):

The arguments are all 1D numpy arrays. For grid type data these should all be of the same length, or left as None. While element type data can be programatically generated and stored in a MagSLD object it is significantly more complicated and the details are not given here. The arguments are respectively:

The \(x\), \(y\) and \(z\) coordinates of the realspace positions of the pixels

The nuclear SLD

The \(x\), \(y\) and \(z\) components of the magnetic SLD

The volume of each pixel. Note that grid type data is expected to be on a regular grid - so if vol_pix is None the volumes are all taken to be the same.

The following code recreates the default data of the scattering calculator GUI, a rectangular grid of 10x10x10 pixels, with each pixel being 6x6x6Å. Each pixel has a constant nuclear SLD of 6.97x10^-6Å^-2 and no magnetic SLD:

import numpy as np
STEPSIZE=6
NODES=10
points = np.linspace(0, STEPSIZE*NODES, NODES, endpoint=False)
pos_x, pos_y, pos_z = np.meshgrid(points, points, points)
pos_x = pos_x.flatten()
pos_y = pos_y.flatten()
pos_z = pos_z.flatten()
data = sas_gen.MagSLD(pos_x, pos_y, pos_z, np.full_like(pos_x, 6.97e-06))

2) Model creation¶

Once we have created our data, we create a GenSAS model to carry out the computation. We can simply create an instance of the GenSAS class and load in our MagSLD object:

model = sas_gen.GenSAS()
model.set_sld_data(data)

Further, we are free to set a number of experiment parameters stored in a dictionary as follows:

model.params["Up_theta"] = 90
model.params["Up_phi"] = 45
...

The parameters correspond exactly to the available input options in the GUI:

scale

background

solvent_SLD

total_volume

Up_frac_in

Up_frac_out

Up_theta

Up_phi

The meanings are identical to those given in the GUI description, although the following should be noted:

The total_volume parameter will be reset to a calculated value everytime the GenSAS.set_sld_data() method is called. If volume correction is needed then the total_volume parameter must be reset.

Up_theta and Up_phi remain in degrees as in the GUI - the conversion to radians is handled within the model.

The rotations between different coordinate systems can also be set using the GenSAS.set_rotations() method which takes optional arguments uvw_to_UVW and xyz_to_UVW, which are the rotations between the \(xyz\), \(uvw\), and \(UVW\) coordinates (see LINK). The rotation matrices are given for the COMPONENTS of the vectors - that is xyz_to_UVW transforms the components of a vector from the \(xyz\) to the \(UVW\) frame. This is the same rotation that transforms the basis vectors from \(UVW\) to \(xyz\). The rotations are given as instances of scipy.spatial.transform.Rotation, and default to the identity. For example if we know the rotation of the sample coordinates as (intrinsic \(ZYZ\) convention) euler angles:

from scipy.spatial.transform import Rotation
import math
theta = math.pi/2.0
phi = math.pi/2.0
chi = 0.0
r = Rotation.from_euler("ZYZ", [theta, phi, chi])
model.set_rotations(xyz_to_UVW=r)

3) Intensity calculation¶

As in the GUI two different types of calculation can be carried out. A full 2D scattering pattern can be calculated in the \(UV\) plane with \(Q_x\) along the \(U\) axis and \(Q_y\) along the \(V\) axis, or a 1D Debye average can be calculated. Unlike in the GUI, while scripting we have precise control over which points are evaluated.

In order to calculate the scattering intensity at a set of \(\mathbf{Q}\) values, we create two lists Qx = [Q_x1, Q_x2, …] and Qy = [Q_y1, Q_y2, …] and pass these into model.runXY([Qx, Qy]). Note that we are passing a nested list of the two lists, i.e. a list of length two, where each element is a list of the same length giving Qx and Qy values. For example to evaluate the scattering intensity on a grid:

x_vals = np.linspace(-5, 5, 10)
y_vals = np.linspace(-5, 5, 10)
xs, ys = np.meshgrid(x_vals, y_vals)
xs = xs.flatten()
ys = ys.flatten()
output = model.runXY([xs, ys])

The output will be the scattering intensities as an array corresponding to the given \(Q\) coordinates.

If we have grid type data with no magnetic component we can calculate the Debye full average at any magnitude \(Q\). Similarly we pass these magnitudes into the model as a list of lists. The first element should be a list of magnitudes, and the second element an empty list:

q_vals = np.linspace(0, 5, 10)
output = model.run([q_vals, []])

Note the difference between the following two code snippets:

Qs = np.linspace(0, 5, 10)
output = model.runXY([Qs, np.zeros_like(Qs)])

Qs = np.linspace(0, 5, 10)
output = model.runXY([Qs, []])

The first calculates the values of the scattering intensity along the positive \(Q_x\) axis. The second calculates the orientational average intensity at various magnitudes of \(Q\).

Examples¶

Scripting Example: Orientational Averaging of the Default Data (Jupyter Notebook)

Scripting Example: Orientational Averaging of the Default Data (PDF)

References¶

[1]
An implementation of an efficient direct Fourier transform of polygonal areas and volumes (2021) Brian B. Maranville arXiv:2104.08309

[2]
Polarization Analysis of Thermal-Neutron Scattering (1969) R. M. Moon, T. Riste, and W. C. Koehler Phys. Rev. 181, 920 DOI

Document History

2015-05-01 Steve King
2021-09-14 Robert Bourne
2023-10-30 Yun Liu